A Feature Fusion Model for Mesoscale Eddy Identification Based on Multi-Source Data
-
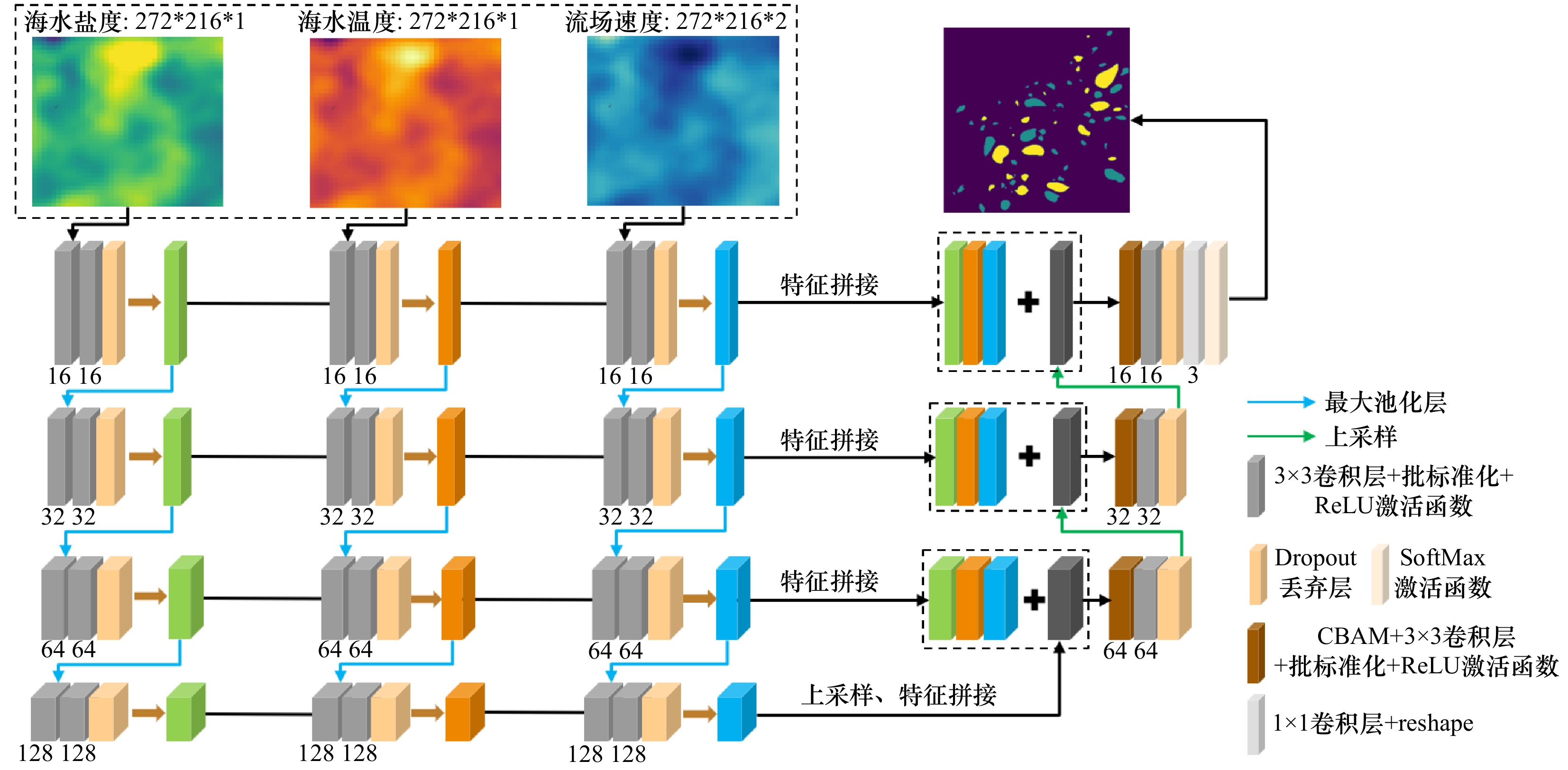
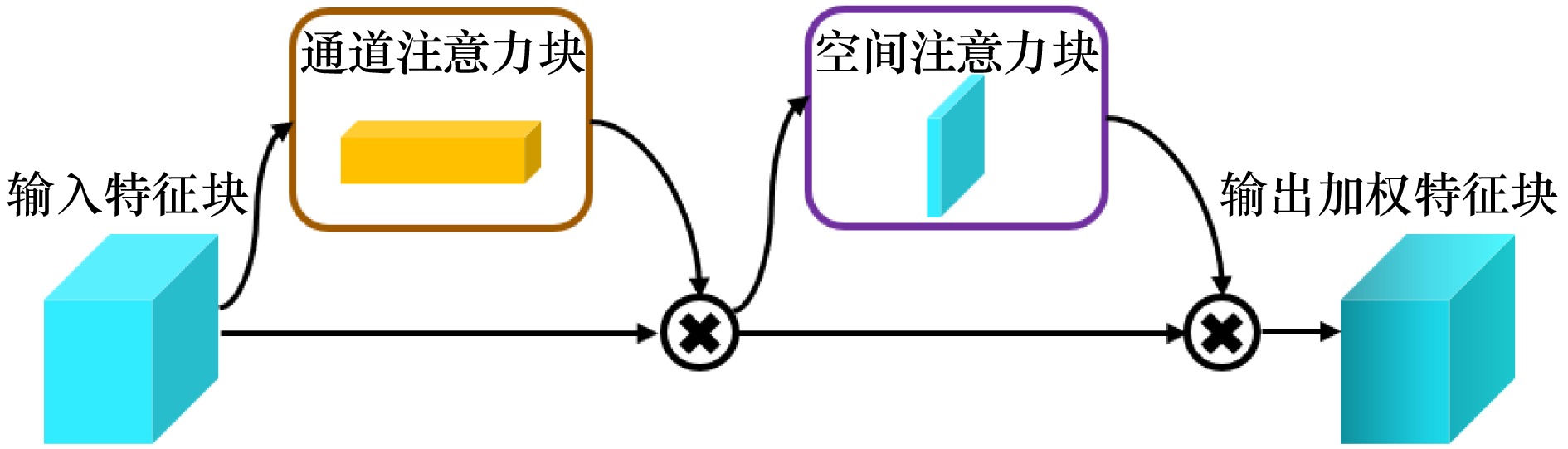
摘要: 中尺度涡作为海洋中的一种重要现象，显著影响着其所在区域的水体分布和物质输送。获取中尺度涡的三维分布情况对海洋资源开发、海洋运输和军事领域具有重要意义。然而，现有的中尺度涡智能识别模型通常依赖于海面高度、海表温度等海面数据，仅用于对海洋表面的中尺度涡进行识别。本文提出了一种基于流场、温度和盐度多源数据的多尺度特征自适应融合模型。在编码器阶段，模型利用多分支结构对多源数据独立地提取特征；在解码器阶段，利用注意力机制对各分支的多层特征进行加权自适应融合；训练过程中采用分类概率梯度损失与Dice系数损失相结合的混合损失函数，提高了模型的识别准确率。利用中国南海区域的数据进行实验验证，模型的全局准确率达到了98.49%，平均Dice系数为
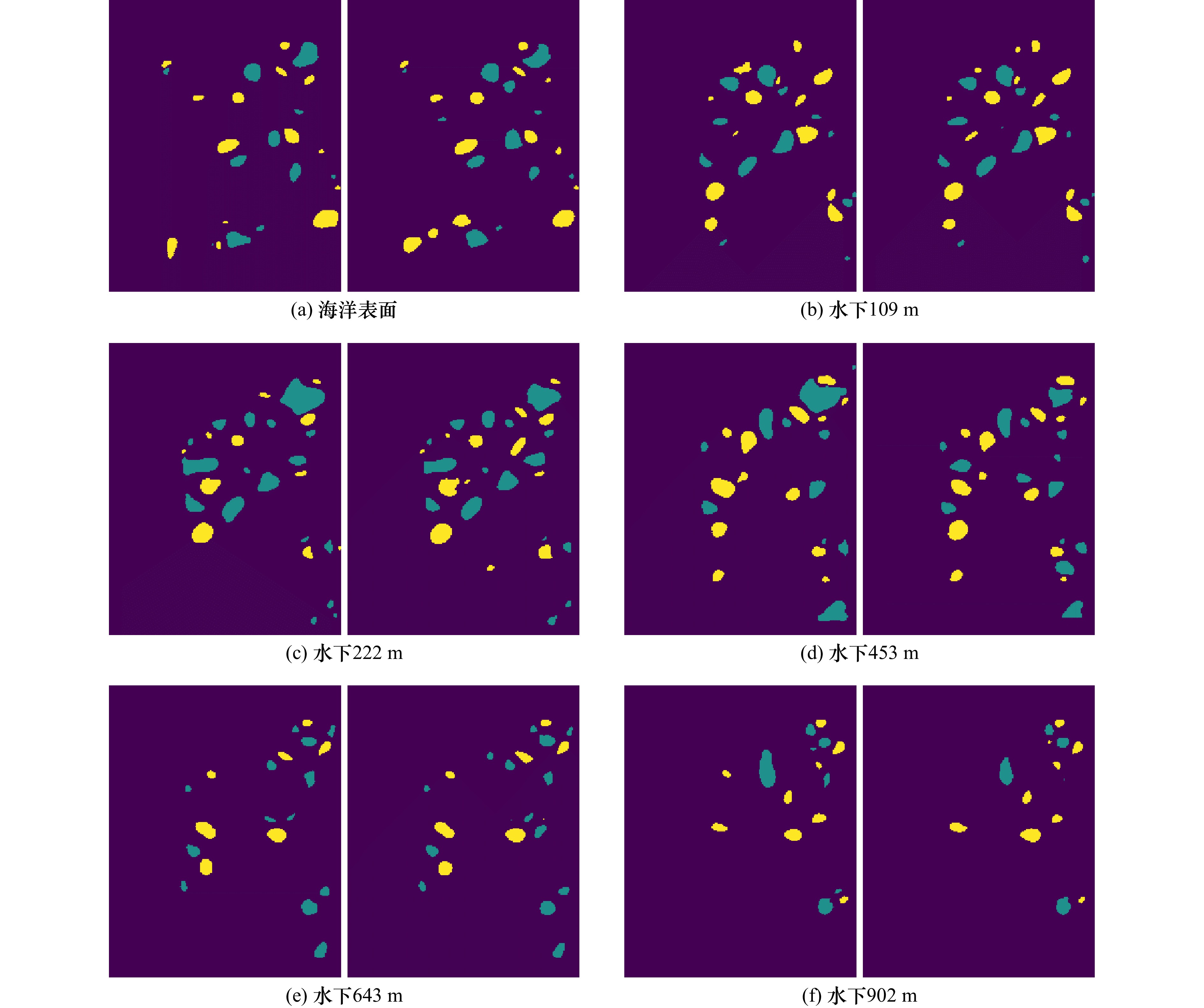
0.8777 ，加权Dice系数为0.8225 ，表明模型在识别海洋表层和不同水深中尺度涡分布的有效性及高准确性。Abstract: Mesoscale eddies, as an important phenomenon in the ocean, significantly influence the distribution of water masses and material transport within their regions. Obtaining the three-dimensional distribution of mesoscale eddies is of great significance for marine resource development, maritime transportation, and military applications. However, existing intelligent identification models for mesoscale eddies typically rely on sea surface data such as sea surface height and sea surface temperature, and are only used to identify mesoscale eddies at the ocean surface. This paper proposes a multi-scale feature adaptive fusion model based on multi-source data, including flow fields, temperature, and salinity. In the encoder stage, the model uses a multi-branch structure to independently extract features from the multi-source data. In the decoder stage, an attention mechanism is employed to perform weighted adaptive fusion of multi-layer features from each branch. During training, a hybrid loss function combining classification probability gradient loss and Dice coefficient loss is used to improve the identification accuracy of the model. Experimental validation is conducted using data from the South China Sea region. The model achieves a global accuracy of 98.49%, an average Dice coefficient of0.8777 , and a weighted Dice coefficient of0.8225 , demonstrating the model’s effectiveness and high accuracy in identifying the distribution of mesoscale eddies at both the sea surface and various water depths.-
Key words:
- mesoscale eddies /
- eddy identification /
- multi-source data /
- multi-scale feature fusion
-
图 4 不同方案对水深55 m涡旋的识别效果对比（海水盐度的单位为千分比，海水温度的单位为摄氏度，结果图中的蓝绿色块为气旋涡、黄色块为反气旋涡）
Fig. 4 Performance comparison of different approaches for eddy identification at 55 m depth (Salinity in ‰, Temperature in ℃, Blue-green areas denote cyclonic eddies; yellow areas denote anticyclonic eddies)
图 5 不同深度的涡旋识别结果图（子图的左侧为真实标注图、右侧为模型识别图，结果图中的蓝绿色块为气旋涡、黄色块为反气旋涡）
Fig. 5 Identification of eddies at different depths (Subfigure left: ground truth; Subfigure right: model results. Blue-green areas denote cyclonic eddies; yellow areas denote anticyclonic eddies)
图 7 HYCOM数据中不同深度的涡旋识别结果图（子图中上半部分为真实标注图、下半部分为模型识别图，蓝绿色块为气旋涡、黄色块为反气旋涡）
Fig. 7 Identification of eddies at different depths in HYCOM dataset (Subfigure upper: ground truth; Subfigure lower: model identification. Blue-green areas denote cyclonic eddies; yellow areas denote anticyclonic eddies)
表 1 模型涡旋识别性能对比
Tab. 1 Model performance comparison for eddy identification
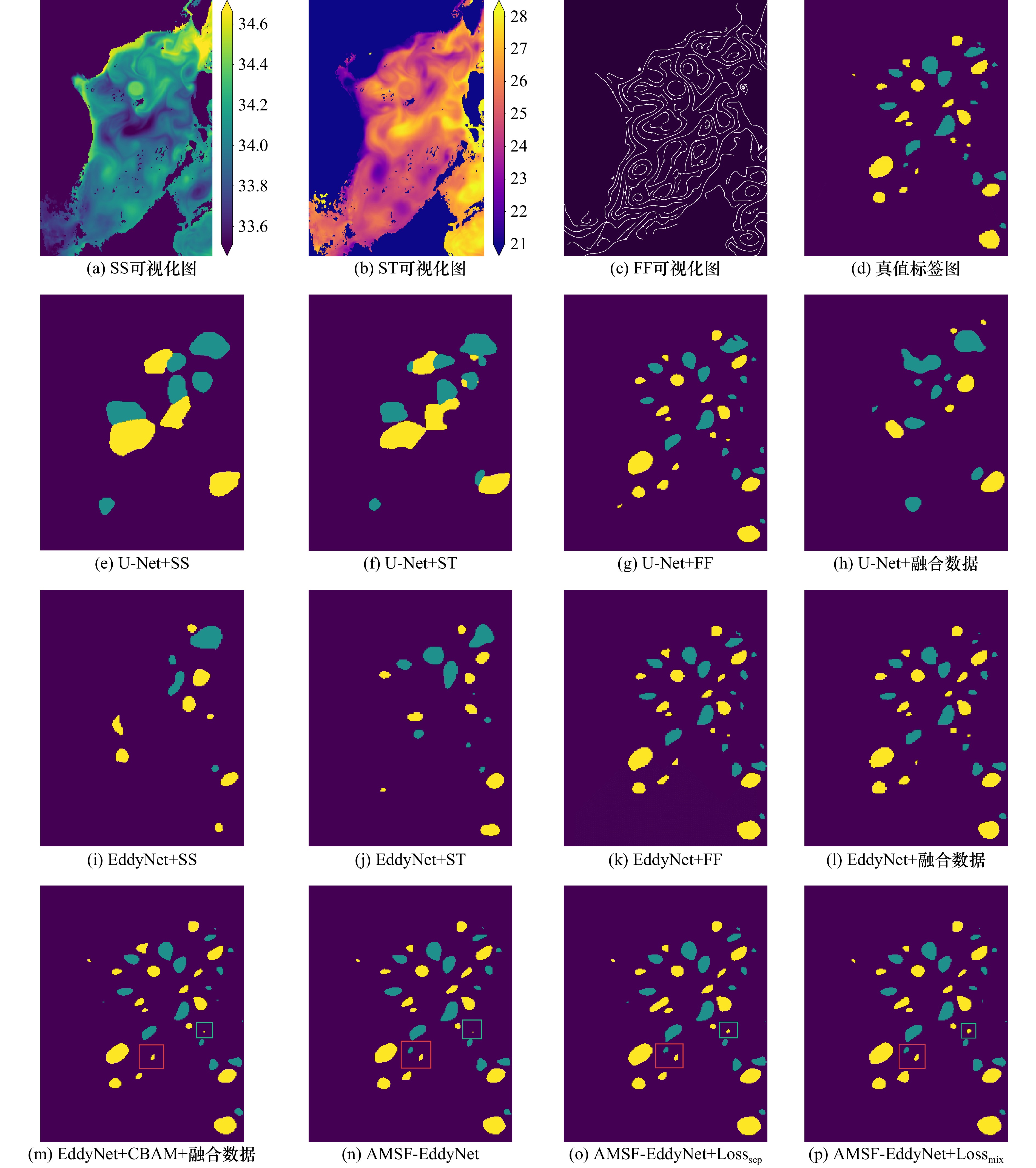
模型 全局准确率 平均Dice系数 加权Dice系数 U-Net+SS 0.8700 0.3904 0.1283 U-Net+ST 0.8804 0.3977 0.1364 U-Net+FF 0.9828 0.8578 0.7935 U-Net+融合数据 0.9239 0.4085 0.1416 EddyNet+SS 0.9480 0.4354 0.1755 EddyNet+ST 0.9570 0.5895 0.4022 EddyNet+FF 0.9838 0.8720 0.8143 EddyNet+融合数据 0.9826 0.8556 0.7902 EddyNet+CBAM+融合数据 0.9832 0.8569 0.7920 AMSF-EddyNet 0.9843 0.8729 0.8154 AMSF-EddyNet+Losssep 0.9846 0.8774 0.8221 AMSF-EddyNet+Lossmix 0.9849 0.8777 0.8225 注：加粗数字为最佳结果 
下载: 导出CSV
表 2
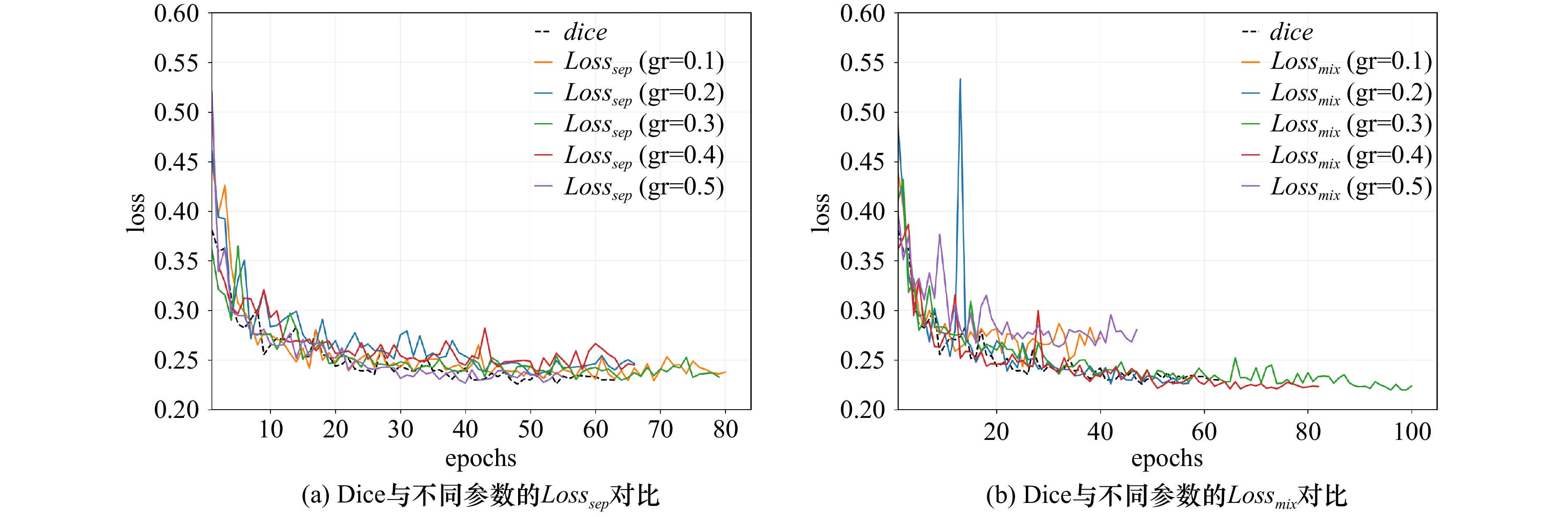
$ {Loss}_{sep} $ 混合损失函数权重参数对比实验Tab. 2 Comparison experiment of
$ {Loss}_{sep} $ weight parameters权重$ \mathit{\sigma } $ 全局准确率 平均Dice系数 加权Dice系数 0 0.9843 0.8729 0.8154 0.1 0.9844 0.8750 0.8186 0.2 0.9846 0.8774 0.8221 0.3 0.9845 0.8776 0.8225 0.4 0.9838 0.8699 0.8112 0.5 0.9847 0.8739 0.8169 1.0 0.9590 0.2280 0.0877
下载: 导出CSV
表 3
$ {Loss}_{mix} $ 混合损失函数权重参数对比实验Tab. 3 Comparison experiment of
$ {Loss}_{mix} $ weight parameters权重$ \mathit{\sigma } $ 全局准确率 平均Dice系数 加权Dice系数 0 0.9843 0.8729 0.8154 0.1 0.9845 0.8760 0.8200 0.2 0.9848 0.8782 0.8232 0.3 0.9842 0.8723 0.8147 0.4 0.9849 0.8777 0.8225 0.5 0.9825 0.8461 0.7763 1.0 0.9617 0.2187 0.0819
下载: 导出CSV
表 4 模型在HYCOM数据集中的涡旋识别性能
Tab. 4 Model eddy identification performance in HYCOM dataset
模型 全局准确率 平均Dice系数 加权Dice系数 AMSF-EddyNet 0.9752 0.8124 0.7282 AMSF-EddyNet+Losssep 0.9748 0.8166 0.7345 AMSF-EddyNet+Lossmix 0.9752 0.8172 0.7353
下载: 导出CSV
-
[1] Dong Changming, Liu Lingxiao, Nencioli F, et al. The near-global ocean mesoscale eddy atmospheric-oceanic-biological interaction observational dataset[J]. Scientific Data, 2022, 9(1): 436. doi: 10.1038/s41597-022-01550-9 [2] Chelton D B, Schlax M G, Samelson R M. Global observations of nonlinear mesoscale eddies[J]. Progress in Oceanography, 2011, 91(2): 167−216. doi: 10.1016/j.pocean.2011.01.002 [3] Zhang Zhengguang, Wang Wei, Qiu Bo. Oceanic mass transport by mesoscale eddies[J]. Science, 2014, 345(6194): 322−324. doi: 10.1126/science.1252418 [4] Zimin A V, Atadzhanova O A. Estimation of the characteristics of mesoscale eddies in the basin of the Lofoten depression from satellite and ship observations[J]. Sovremennye Problemy Distantsionnogo Zondirovaniya Zemli iz Kosmosa, 2020, 17(3): 202−210. doi: 10.21046/2070-7401-2020-17-3-202-210 [5] Xie Huarong, Xu Qing, Dong Changming. Deep learning for mesoscale eddy detection with feature fusion of multisatellite observations[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2024, 17: 18351−18364. doi: 10.1109/JSTARS.2024.3468457 [6] Okubo A. Horizontal dispersion of floatable particles in the vicinity of velocity singularities such as convergences[J]. Deep Sea Research and Oceanographic Abstracts, 1970, 17(3): 445−454. doi: 10.1016/0011-7471(70)90059-8 [7] Weiss J. The dynamics of enstrophy transfer in two-dimensional hydrodynamics[J]. Physica D: Nonlinear Phenomena, 1991, 48(2/3): 273−294. [8] Sadarjoen I A, Post F H. Detection, quantification, and tracking of vortices using streamline geometry[J]. Computers & Graphics, 2000, 24(3): 333−341. [9] Nencioli F, Dong Changming, Dickey T, et al. A vector geometry–based eddy detection algorithm and its application to a high-resolution numerical model product and high-frequency radar surface velocities in the Southern California Bight[J]. Journal of Atmospheric and Oceanic Technology, 2010, 27(3): 564−579. doi: 10.1175/2009JTECHO725.1 [10] Xing Tao, Yang Yikai. Three mesoscale eddy detection and tracking methods: assessment for the South China Sea[J]. Journal of Atmospheric and Oceanic Technology, 2021, 38(2): 243−258. doi: 10.1175/JTECH-D-20-0020.1 [11] 张家灏, 邓科峰, 聂腾飞, 等. 基于机器学习的海洋中尺度涡检测识别研究综述[J]. 计算机工程与科学, 2021, 43(12): 2115−2125. doi: 10.3969/j.issn.1007-130X.2021.12.004Zhang Jiahao, Deng Kefeng, Nie Tengfei, et al. Overview on ocean mesoscale eddy detection and identification based on machine learning[J]. Computer Engineering and Science, 2021, 43(12): 2115−2125. doi: 10.3969/j.issn.1007-130X.2021.12.004 [12] 徐广珺, 施宇诚, 余洋, 等. 海洋涡旋智能检测研究进展[J]. 海洋学研究, 2024, 42(3): 38−50. doi: 10.3969/j.issn.1001-909X.2024.03.003Xu Guangjun, Shi Yucheng, Yu Yang, et al. Recent developments in AI-based oceanic eddy identification[J]. Journal of Marine Sciences, 2024, 42(3): 38−50. doi: 10.3969/j.issn.1001-909X.2024.03.003 [13] Xu Guangjun, Cheng Cheng, Yang Wenxian, et al. Oceanic eddy identification using an AI scheme[J]. Remote Sensing, 2019, 11(11): 1349. doi: 10.3390/rs11111349 [14] Lguensat R, Sun Miao, Fablet R, et al. EddyNet: a deep neural network for pixel-wise classification of oceanic eddies[C]//Proceedings of 2018 IEEE International Geoscience and Remote Sensing Symposium. Valencia, Spain: IEEE, 2018: 1764−1767. [15] Pegliasco C, Delepoulle A, Mason E, et al. META3.1exp: a new global mesoscale eddy trajectory atlas derived from altimetry[J]. Earth System Science Data, 2022, 14(3): 1087−1107. doi: 10.5194/essd-14-1087-2022 [16] Sun Xin, Zhang Meng, Dong Junyu, et al. A deep framework for eddy detection and tracking from satellite sea surface height data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 59(9): 7224−7234. doi: 10.1109/TGRS.2020.3032523 [17] 董子意. 基于深度学习的海洋中尺度涡自动检测模型[D]. 杭州: 浙江大学, 2021.Dong Z Y. An automatic marine mesoscale eddy detection model based on deep learning[D]. Hangzhou: Zhejiang University, 2021. [18] Ronneberger O, Fischer P, Brox T. U-Net: convolutional networks for biomedical image segmentation[C]//Proceedings of the 18th International Conference on Medical Image Computing and Computer-Assisted Intervention. Munich, Germany: Springer, 2015: 234−241. [19] Santana O J, Hernández-Sosa D, Smith R N. Oceanic mesoscale eddy detection and convolutional neural network complexity[J]. International Journal of Applied Earth Observation and Geoinformation, 2022, 113: 102973. doi: 10.1016/j.jag.2022.102973 [20] Xu Guangjun, Xie Guangjun, Dong Changming, et al. Application of three deep learning schemes into oceanic eddy detection[J]. Frontiers in Marine Science, 2021, 8: 672334. doi: 10.3389/fmars.2021.672334 [21] Moschos E, Kugusheva A, Coste P, et al. Computer vision for ocean eddy detection in infrared imagery[C]//Proceedings of 2023 IEEE/CVF Winter Conference on Applications of Computer Vision. Waikoloa, HI, USA: IEEE, 2023: 6384−6393. [22] Liu Yingjie, Zheng Quanan, Li Xiaofeng. Characteristics of global ocean abnormal mesoscale eddies derived from the fusion of sea surface height and temperature data by deep learning[J]. Geophysical Research Letters, 2021, 48(17): e2021GL094772. doi: 10.1029/2021GL094772 [23] Xie Huarong, Xu Qing, Dong Changming. Deep learning for mesoscale eddy detection with feature fusion of multisatellite observations[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2024, 17: 18351−18364. (查阅网上资料, 本条文献和第5条文献重复, 请核对) [24] 李忠伟, 刘格格, 李永, 等. 基于多模态数据融合的改进中尺度涡检测模型[J]. 海洋预报, 2024, 41(2): 53−62, doi: 10.11737/j.issn.1003-0239.2024.02.006Li Zhongwei, Liu Gege, Li Yong, et al. An improved mesoscale eddy detection model based on multimodal data fusion[J]. Marine Forecasts, 2024, 41(2): 53−62, doi: 10.11737/j.issn.1003-0239.2024.02.006 [25] Huo Jidong, Zhang Jie, Yang Jungang, et al. High kinetic energy mesoscale eddy identification based on multi-task learning and multi-source data[J]. International Journal of Applied Earth Observation and Geoinformation, 2024, 128: 103714. doi: 10.1016/j.jag.2024.103714 [26] 王丽娜, 孙阳, 张红春, 等. 基于注意力的多尺度残差U-Net的海洋中尺度涡检测[J]. 海洋与湖沼, 2025, 56(1): 64−76.Wang Lina, Sun Yang, Zhang Hongdong, et al. A multi-scale attention residual-based U-Net model for detection of ocean mesoscale eddies[J]. Oceanologia et Limnologia Sinica, 2025, 56(1): 64−76. [27] Xing Jin, Wang Feng, Yang Dongkai, et al. Detection and estimation of daily oceanic mesoscale eddies from spaceborne global navigation satellite system-reflectometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2025, 63: 5800816. [28] Milletari F, Navab N, Ahmadi S A. V-Net: fully convolutional neural networks for volumetric medical image segmentation[C]//Proceedings of 2016 Fourth International Conference on 3D Vision. Stanford, CA, USA: IEEE, 2016: 565−571. [29] Lin Xiayan, Zhao Hui, Liu Yu, et al. Ocean eddies in the Drake Passage: decoding their three-dimensional structure and evolution[J]. Remote Sensing, 2023, 15(9): 2462. doi: 10.3390/rs15092462 [30] Liu Chang, Lin Xiayan, Xu Guangjun, et al. Improved identification and tracking of three-dimensional eddies in the Southern Ocean utilizing 3D-U-Res-Net[J]. Frontiers in Marine Science, 2024, 11: 1482804. doi: 10.3389/fmars.2024.1482804 [31] 丁雅楠, 石绥祥, 刘克修, 等. 基于高分辨率再分析海流数据的三种涡旋识别方法在南海的评估[J]. 海洋通报, 2024, 43(3): 301−311.Ding Yanan, Shi Suixiang, Liu Kexiu, et al. Assessment of three eddy detection methods based on high-resolution reanalysis of ocean current data in the South China Sea[J]. Marine Science Bulletin, 2024, 43(3): 301−311. [32] Woo S, Park J, Lee J Y, et al. CBAM: convolutional block attention module[C]//Proceedings of the 15th European Conference on Computer Vision. Munich, Germany: Springer, 2018: 3−19. -
图(7) / 表(4)
计量
- 文章访问数: 22
- HTML全文浏览量: 4
- PDF下载量: 4
- 被引次数: 0
