Study on the recovery process and the main controlling factors for post-storm beach profiles of a headland bay: Taking the Narrabeen Beach in Australia as an example
-
摘要: 位于澳洲悉尼附近的Narrabeen海滩经历着较频繁的风暴浪侵袭,在鲜有人工干预下,该海滩具有从风暴期间的沙坝剖面到常浪期稳定的滩肩剖面交替演变的自适应特征。为探明Narrabeen海滩在经历风暴浪后的自恢复动力,本文通过该海滩多年连续实测资料,分析典型风暴浪过后海滩剖面在常浪作用下的演变规律以及在恢复过程中的主要水动力要素。研究结果表明:Narrabeen海滩的恢复速率存在沿岸差异,沙滩中部恢复速率最快;在常年SE浪向主导下,小波高长周期波浪对北部以及中部剖面的恢复起促进作用,而潮动力对南部剖面在恢复期内的动态响应调控作用更强。本文据此提出考虑潮差的累积波能概念,发现其与南部海滩恢复能力间有良好的相关性。经调查,地形造成的浪向变化以及各剖面的地质地貌特征是造成该岬湾海滩恢复效率和恢复动力空间差异性的主要原因。此外,从年际时间尺度看,风暴剖面的恢复能力还受控于南方涛动因子。本文的研究方法和结论可为在极端海洋动力下岬湾海滩的防灾减灾和灾后修复提供有益借鉴。Abstract: Narrabeen Beach, located Sydney, Australia, has undergone frequent storm wave events. The beach form has an adaptive ability to evolve from storm profile to berm profile with little human intervention. In order to investigate the self-recovery capability of the headland bay after storm waves, this paper analyzes how beach evolves during the post-storm calm weathers and identify the main hydrodynamic factors that dominate the beach recovery based on the multi-year continuous measurement data of Narrabeen Beach. The results show that there are spatial differences along the shore in the recovery rates, with the fastest recovery rate in the middle of the beach. Besides, southeast breezes with small wave-height and long wave-period contribute most to the storm-profiles’ recovery, especially to the northern-to-central portion. Whilst for the southern part of the headland bay tidal force modulate the beach recovery efficiency more. Accordingly, a concept of cumulative wave energy considering tidal range is proposed by this study and found to well correlated with the self-recovery ability of the southern beach profile. Through investigation, variation of wave directions induced by topography, along with geological and geomorphological features all play a vital role on the spatial inhomogeneity of the recovery efficiency for the headland bay. In addition, from the secular time scale, the recovery ability of the storm profiles is also controlled by the Southern Oscillation Index. The analysis and findings of this paper can provide useful references for disaster prevention and mitigation, and post-disaster protection and restoration for a headland bay under extreme sea forces.
-
1. 引言
砂质海岸作为宝贵的海岸带资源,支撑着滨海地区旅游业,带动着滨海城市的发展。与此同时,砂质海岸也是受风暴侵袭的脆弱地带,一次风暴所释放的能量会对滨海旅游资源及基础设施带来严重破坏。一般来说,受风暴侵蚀后的砂质海岸会在常浪期自然恢复力下进行自我修复。此外,定期的海滩养护及人工沙滩建设,也可以增加海岸带韧性[1]。因此,大部分海滩常年处于风暴剖面和滩肩剖面交替的动态平衡状态。
岬湾海滩是最常见的沙滩形式,近岸水动力受地形影响较平直岸线复杂。例如,岬角处波浪的辐聚、绕射和破碎,岬湾常见的沿岸流和离岸流以及沿岸不均匀的坡度变化不仅会影响泥沙输运,也会调控潮间带与潮下带之间泥沙交换[2–3]。不少学者通过观测数据、数模反演或物理模型试验等方法研究了单个风暴或风暴群过境后海滩的冲淤特性[4–5],但多数研究多集中于平直海滩或单一剖面。然而对于岬湾海滩,风暴过后,沿岸存在较强的冲淤不均性,且各剖面恢复机理不完全一致,这为预测风暴后海滩的恢复能力带来困难。因此,剖析岬湾海滩各剖面常浪期的恢复过程和主要恢复动力,对灾后岬湾海滩的修复工作具有重要意义。下文中,笔者基于Narrabeen岬湾海滩多年实测剖面资料,结合该海域的水文资料,分析海滩不同位置处风暴后的恢复动力,解析影响各剖面恢复过程的主要原因,以期为相似海滩的风暴侵蚀防控管理和灾后修复提供参考。
2. 研究地点与水动力特征
2.1 研究地点
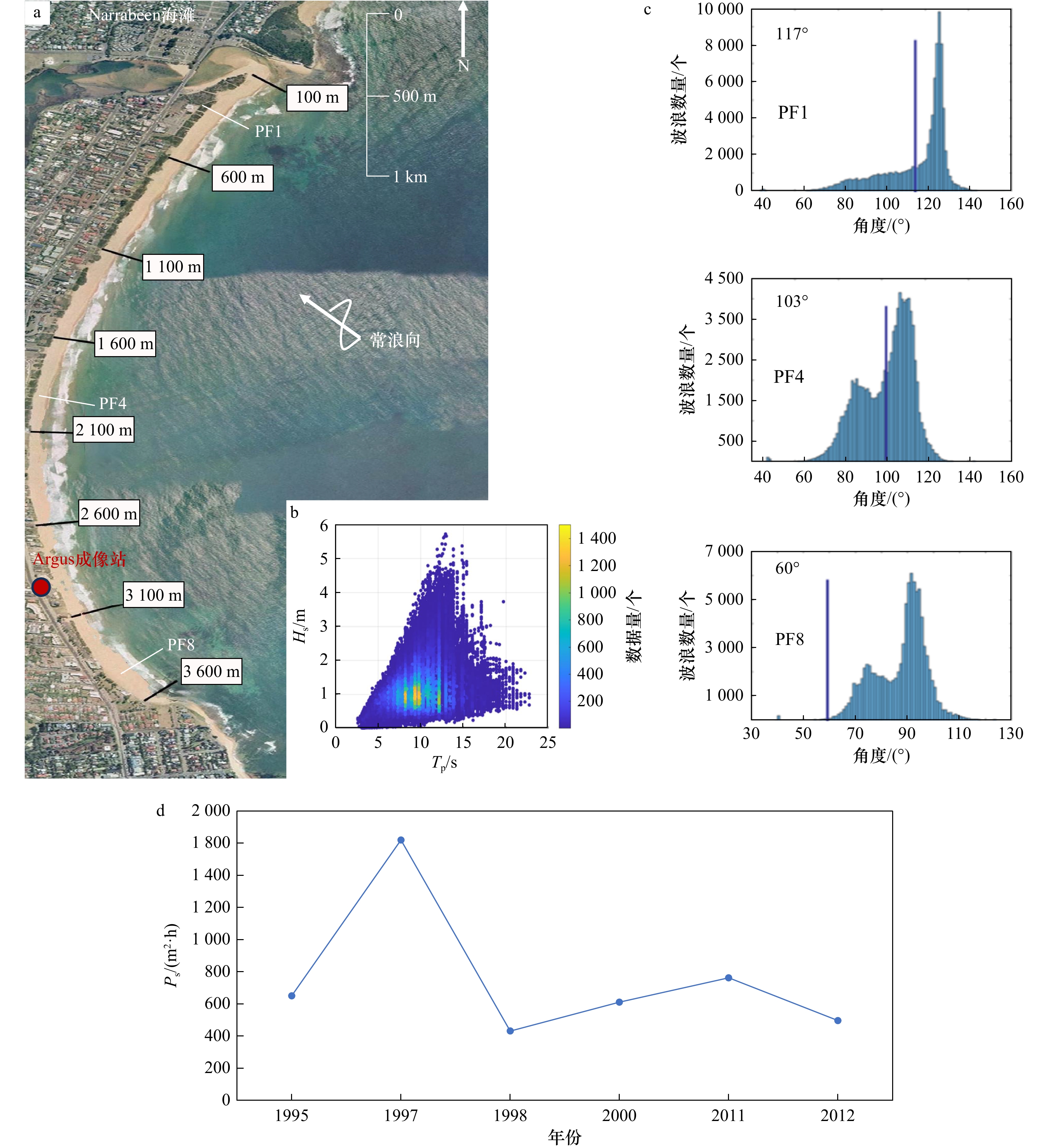
澳大利亚东南沿岸分布着700余个平均长度约为1.3 km的岬湾砂质海滩,其地貌特征多为南北走向,两端为基岩质岬头,中间凹入段为砂质海滩,且经常受到风暴浪的侵袭。Narrabeen海滩是其中一处典型的岬湾砂质海滩,位于悉尼北部,长约3.6 km(图1a)。1976年4月,悉尼大学 (澳大利亚)Andrew Short教授和他的志愿者团队开始了每月一次延续至今的海滩剖面调查计划,Narrabeen海滩也因此成为世界上为数不多的不间断海滩监测点。该调查项目自2016年4月起免费对全球公开发布海滩剖面的监测数据(http://Narrabeen.wrl.unsw.edu.au)和相关波浪和潮流数据,以支持各地研究者们更深入地探索以Narrabeen海滩为例的砂质海滩地貌演变特征[6]。
2.2 地形数据
Narrabeen海滩的地形监测采用跨岸监测,每次测量的跨岸间距为10 m,延伸至平均海平面以下1~4 m。1976−2006年悉尼大学的海岸研究组采用Emery方法进行调查,自2004年开始,新南威尔士大学(UNSW)水动力实验室开始从Emery方法过渡到具有高精度的RTK-GPS技术,跨岸分辨率提高到0.1 m。本文采用的地形数据取自该海滩自北向南分布的3处代表性剖面:PF1、PF4和PF8(图1a),数据起止年份分别为1995年和2011年,各剖面地形的时间间隔约为1个月。
此外,UNSW的研究小组在一座滨海公寓楼顶上设立了Argus海岸成像站。该成像站位于海拔44 m处,由一组监控摄像机组成,在白天每30 min收集一套图像,进行长期海滩监测,并同时配套有远程图像采集系统和中央操作服务器两个子系统。Narrabeen海滩的图像信息通过UNSW的研究小组在Water Research Laboratory (WRL) Coastal Imaging 主页(http://ci.wrl.unsw.edu.au/)对全球发布。本文利用Argus海滩成像辅以分析岸线演变的整体态势。
2.3 水动力数据
本文采用的潮位资料来源于附近HMAS验潮站(33°49′31.66″S,151°15′30.71″E),时间分辨率为15 min。Narrabeen海滩位于中等强度潮动力作用区,年平均潮差在2 m 左右。波浪数据来自澳大利亚天气与气候研究中心(CAWCR)的后报数据(http://new.mhl.nsw.gov.au/),包括:有效波高(
$ {H}_{\mathrm{s}} $ )、谱峰周期($ {T}_{\mathrm{p}} $ )、平均波向($ {\theta }_{{\mathrm{m}}} $ ),离岸最近至水深10 m处[7]。该后报数据时间分辨率为1 h,空间分辨率为20 m × 30 m。常浪期各剖面波浪的分布规律如图1c所示,浪向计算遵循以正北向为起点,顺指针为正规则。由图可见,整体上各剖面所受常浪向在ESE−E之间,出现频率均可达到30%以上。北部剖面PF1,波向分布呈单峰状,入射波浪主要从ESE向来。而在中部剖面PF4和南部剖面PF8,波向分布呈双峰状,受到E向浪的作用更多,特别是在岬湾中部PF4,波浪主要为垂直入射。近岸波能梯度自北向南传递,一方面由于北部岬角受到南方传播过来的涌浪直接作用,另一方面受南北海岬作用,波能在近岸重新分配[8–10]。
2.4 风暴浪事件和常浪恢复期
Narrabeen海滩所受大浪主要由两部分组成:一部分由SSE向涌浪组成;另一部分大浪又由直接作用于或靠近岸线的气旋造成,出现几率约6%[11–12]。其中,SSE向涌浪为中高能深水波 (
$ {H}_{\mathrm{s}} = 1.6\;{\mathrm{m}} $ 和$ {T}_{\mathrm{p}} $ = 10 s)。这些涌浪通常由位于澳大利亚大陆以南的南塔斯曼海面上传播的中纬度气旋产生,每月发生5~9次,涌浪传播过程中能量汇集,易形成对于岸线有侵蚀作用的风暴浪。波浪资料(图1b)表明,风暴期间的波浪周期集中分布于10~15 s之间,有效波高主要集中在3~4 m之间;而常浪期间普遍为8~12 s,有效波高集中在0.5~1.5 m之间。依据以往研究[11–12],该海滩风暴浪定义为波高大于等于3 m(多年有效波高的95%分位数),单次风暴浪事件的最小持续时间为12 h。本研究选取6起典型风暴浪事件(分别发生在1995年、1997年、1998年、2000年、2011年、2012年),探究风暴过后常浪恢复期间,Narrabeen海滩剖面的恢复过程和恢复动力。Dolan和Davis[13]发现风暴持续时间和最大显著波高对海滩形态动力变率有明显影响,基此,提出了“风暴强度指数(
$ {P}_{{\mathrm{s}}} $ )” :$$ {P}_{{\mathrm{s}}}={H}_{{\mathrm{s}},\;{\mathrm{max}}}^{2}\Delta t \text{,} $$ (1) 式中,
$ {H}_{{\mathrm{s}},\;{\mathrm{max}}} $ 是风暴期间最大有效波高,单位为 m;$ \Delta t $ 是风暴持续时间,单位为h。图1d展示了这6起事件的强度,$ {P}_{{\mathrm{s}}} $ 表明,1997年发生的风暴浪强度指数最大。3. 海滩恢复特征
3.1 一维剖面演变
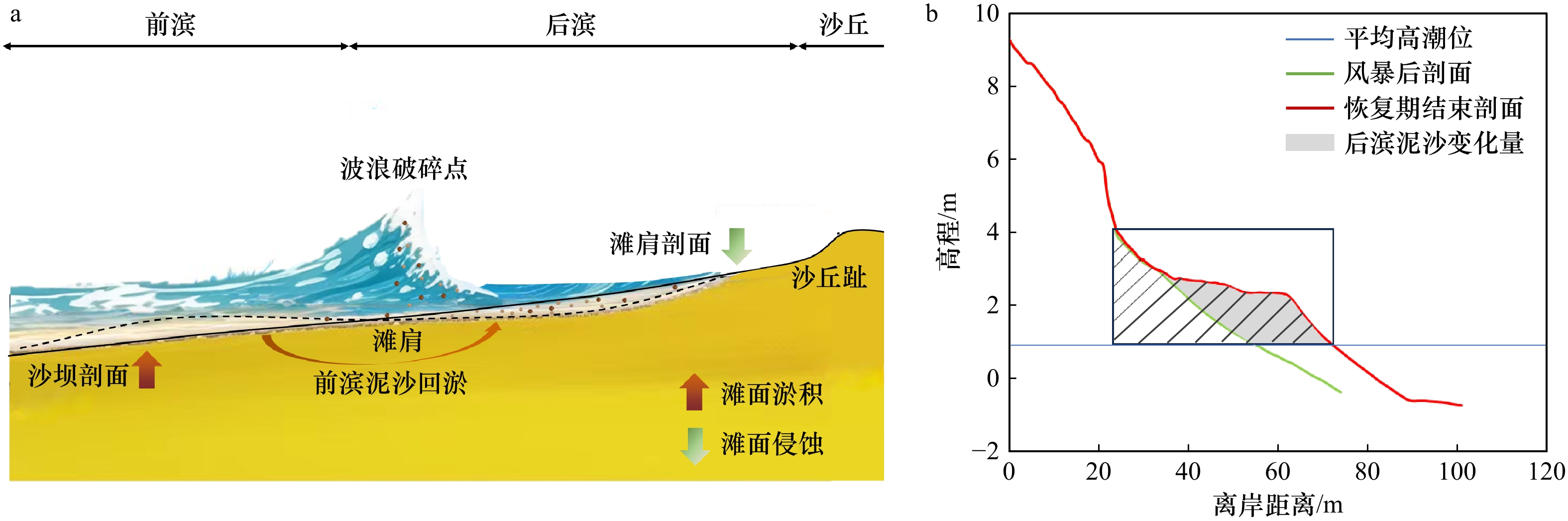
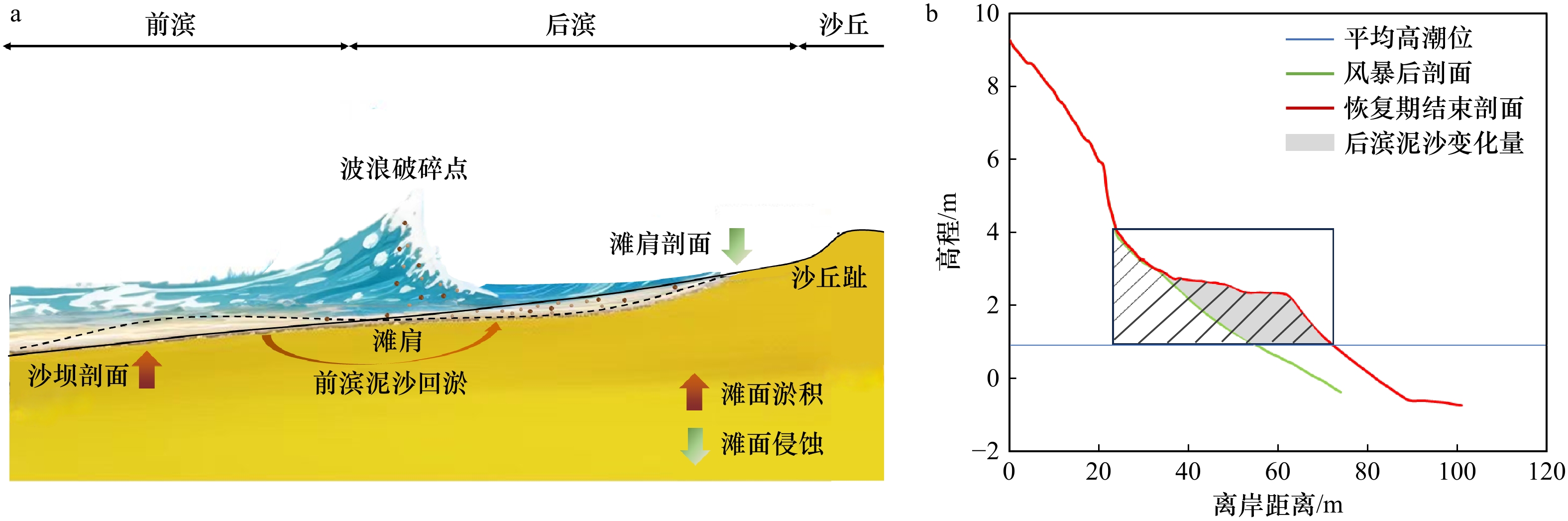
从地貌学角度对海滩剖面进行分段:将平均高潮位至平均低潮位之间区域定义为前滨,平均高潮位到海岸线之间的区域称为后滨,前后滨之间由滩肩作为分界,后滨以上沙体堆积形成沙丘。受风暴作用,平静天气下稳定的滩肩剖面(图2a实线)受到侵蚀,后滨滨面的泥沙被冲刷至外海,于前滨处形成水下沙坝,因此又把风暴剖面称为“沙坝剖面” (图2a虚线)。之后沙坝剖面在常浪期小波作用下逐渐恢复到风暴前滩肩剖面的形态。本文以常浪期后滨滨面单位宽度的泥沙淤积量作为量化海滩恢复程度的指标。图2b阴影部分显示了以PF4为例的后滨滨面泥沙变化量的计算面积。
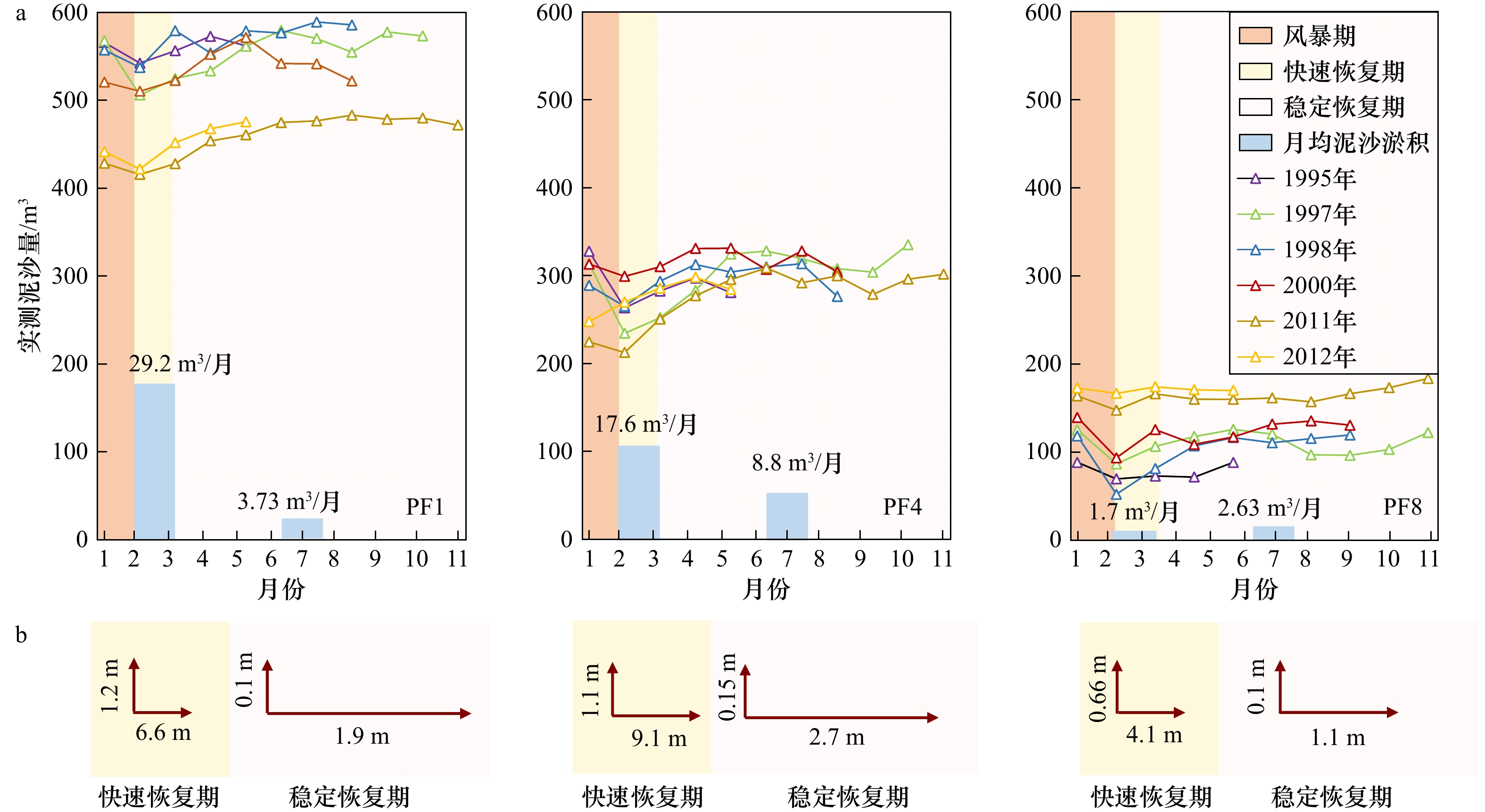
图3a展示了6起典型风暴浪事件前后实测后滨滨面泥沙量(沙丘趾所在垂直切面与最高潮位和剖面包裹的面接,图2b)的变化过程。由图可见,风暴浪事件发生后,各剖面后滨滨面均恢复到风暴前初始状态。海滩北部(PF1)、中部(PF4)、南部(PF8)的后滨普遍遭受侵蚀;除1997年事件以外,常浪期首月内,后滨滨面泥沙侵蚀量可恢复至50%以上。下文将常浪作用第一个月称之为“快速恢复期” ;常浪作用两个月后,后滨滨面呈现冲淤交替的趋势,在连续5个月常浪作用下后滨逐渐趋于稳定,基本恢复甚至超出之前滨面泥沙量。下文中将常浪作用第2个月至下一场风暴来临的时段称为“稳定恢复期”。图3a中柱状图对比了快速恢复期和稳定恢复期后滨滨面实测月均泥沙淤积量。图3b中垂向箭头向上代表恢复期沙丘趾月均高程在抬升,图3b中以沙丘趾抬升高程标定,水平箭头的长度表示岸线月均向海前进量与固定沙丘趾月均抬升高程的比值。由图可见,沙丘趾,即后滨滨面在快速恢复期迅速抬升,而在稳定恢复期,滨面抬升速度放缓,岸线逐步持续向海前进。由图可见,在“快速恢复期”,北部剖面PF1的沙丘趾抬升速率和后滨泥滩面恢复速率最快,中部剖面PF4岸线向海前进速率最快,而南部剖面PF8沙丘趾抬升速率和后滨滩面恢复速率最慢。而在“稳定恢复期” ,中部剖面PF4各项指标的恢复速率均最快。
 图 3 典型风暴事件过后在恢复期的后滨滨面逐月泥沙量时间过程线(a);不同恢复期内,各剖面岸线月均向海前进量与沙丘趾月均抬升量的相对变化对比(b)Figure 3. Time series of the monthly-mean sediment volume on the backshore during the recovery period after each typical storm event (a); comparison of the ratios of the monthly-averaged seaward displacement of the shoreline’s position over the monthly-averaged elevated displacement of the dune toe for each profile during different recovery periods (b)
图 3 典型风暴事件过后在恢复期的后滨滨面逐月泥沙量时间过程线(a);不同恢复期内,各剖面岸线月均向海前进量与沙丘趾月均抬升量的相对变化对比(b)Figure 3. Time series of the monthly-mean sediment volume on the backshore during the recovery period after each typical storm event (a); comparison of the ratios of the monthly-averaged seaward displacement of the shoreline’s position over the monthly-averaged elevated displacement of the dune toe for each profile during different recovery periods (b)3.2 岸线整体冲淤特征
图4对比了风暴期、快速恢复期以及稳定恢复期的海滩成像。通过像素强度聚类技术(PIC)从捕捉到的图像中检测出滩肩、沙丘趾的位置。风暴期间沙丘趾位置沿岸曲折分布,南北岬角处沙丘趾(位置如黑色实线所示)更加接近靠海一侧。快速恢复期,后滨滨面狭窄(滩肩位置如红色虚线所示),稳定恢复期,后滨滨面逐渐宽阔(滩肩位置如蓝色虚线)。
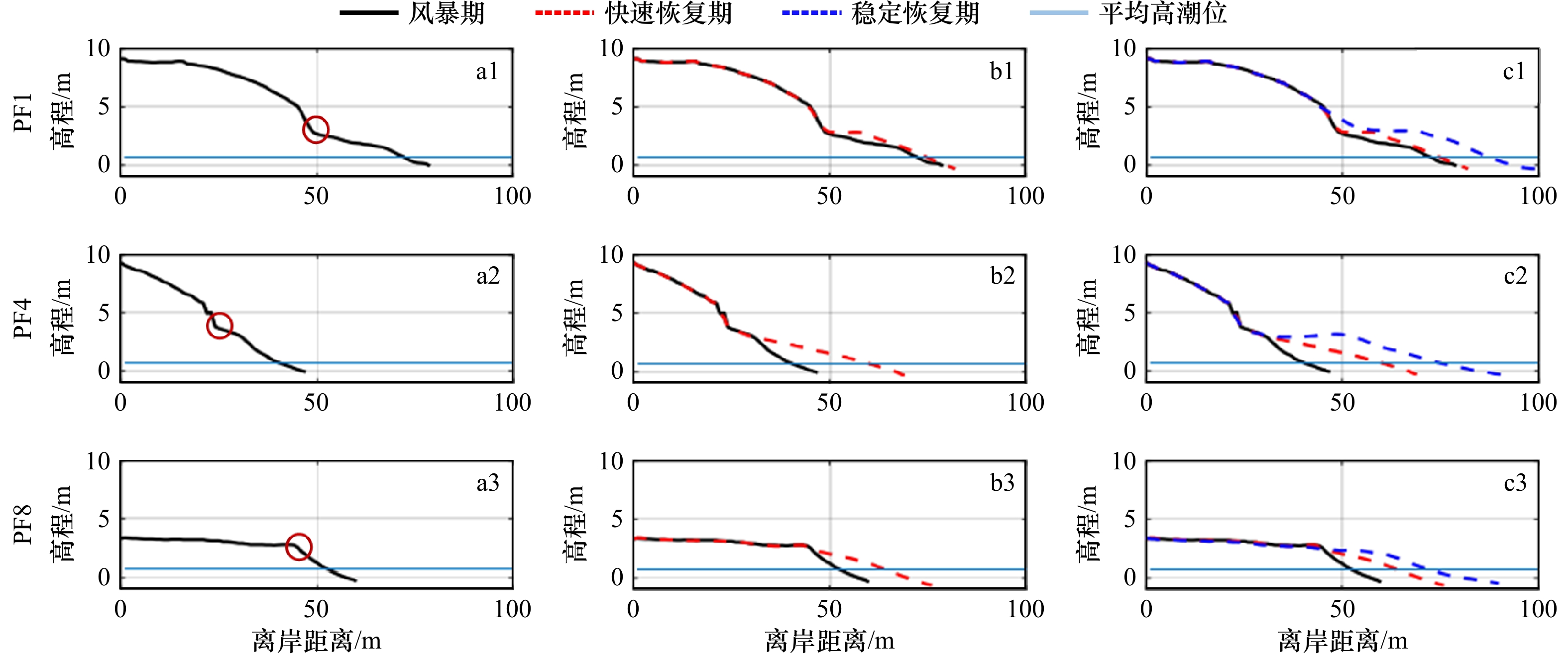
实测剖面分析(图5)显示沙丘顶高度也存在很大的沿岸差异:北部海滩沙丘在平均海平面以上9 m,而南部海滩由于城市发展侵占了大部分的沙丘,高度只有3~4 m。在恢复期,泥沙在后滨滨面逐渐堆积,后滨坡度变缓,并形成滩肩。下文将通过拆解影响海滩演变的水动力要素,结合后滨滨面泥沙恢复量,进行相关性分析,探究影响海滩各处恢复速率的主要因素。
4. 影响海滩演变速率的因素
潮汐交替地暴露和淹没前滨和后滨滨面,并对波浪的传播变形、破碎过程产生影响,后者主导了海滩的泥沙输移。Davis等[14]前期研究发现潮差会对沉积物运输、海滩形态变化的速度以及海滩的波能梯度造成影响;冯曦等[15]发现潮相位对短时间尺度(潮周期内)滨面恢复量起到调控作用。据此,本文综合考虑波能与潮汐对于常浪恢复的共同作用,提出累积波能的概念(
$ {P}_{\mathrm{r}} $ ):$$ {P}_{\mathrm{r}}={\int }_{0}^{D}{\alpha \left({\eta }_{t}\right)H}_{\mathrm{s}}{\left(t\right)}^{2}{\mathrm{d}}t \text{,} $$ (2) 式中,
$ {P}_{{\mathrm{r}}} $ 单位为W;$ {H}_{\mathrm{s}} $ 为有效波高,单位为m;$ t $ 为时间,单位为s;$ {\eta }_{t} $ 代表实时潮位,单位为m;$ \alpha \left({\eta }_{t}\right) $ 是根据潮位而定的权重系数,用以描述潮位对波能的调制作用,$ \alpha \left({\eta }_{t}\right)={\eta }_{t}/{\mathrm{MS}}{\mathrm{R}} $ ,$ {\mathrm{MSR}} $ 为平均大潮潮差,单位为m;式(2)中$ {\mathrm{d}}t $ 取1 h;$ D $ 为持续时间。本文对于海滩恢复期间单位宽度的后滨滨面泥沙变化量与
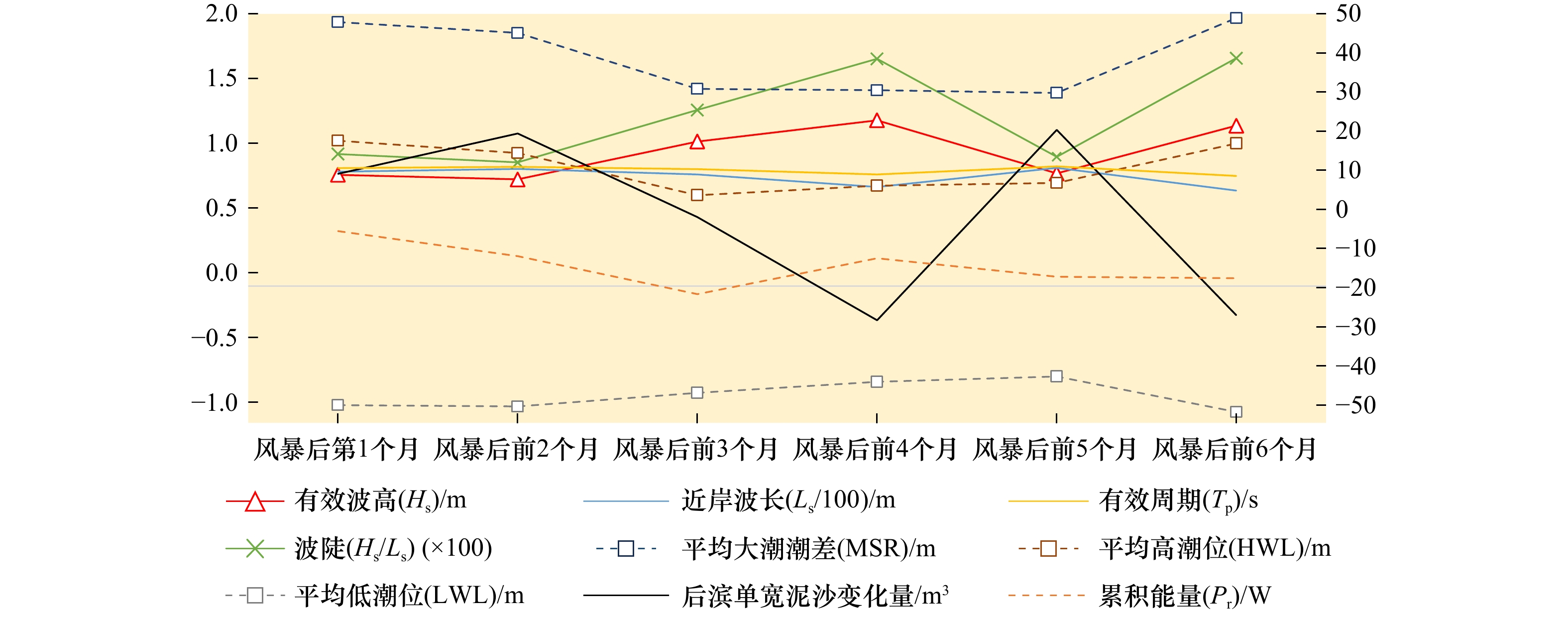
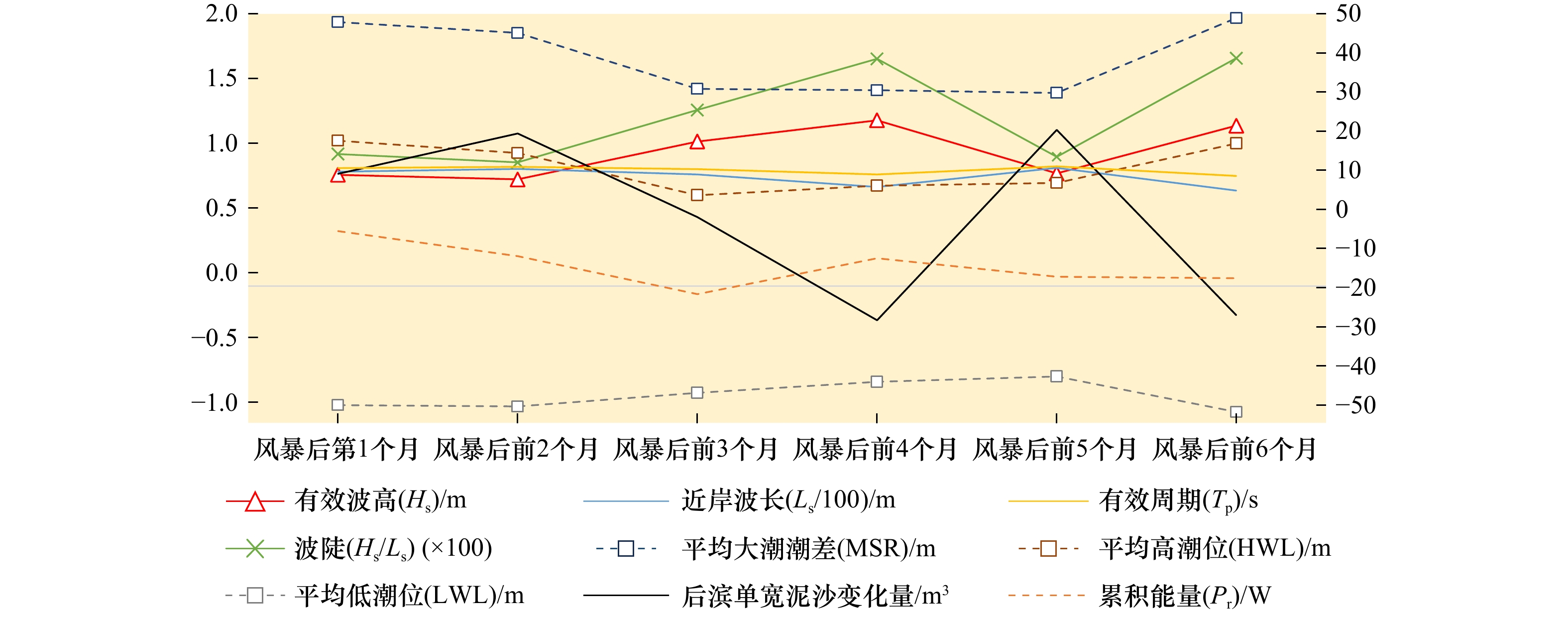
$ {P}_{\mathrm{r}} $ 、$ {H}_{\mathrm{s}} $ 、有效波周期($ {T}_{\mathrm{s}} $ )、有效波长($ {L}_{\mathrm{s}} $ )、波陡($ {H}_{\mathrm{s}}/{L}_{\mathrm{s}} $ )、潮差、潮位等水动力要素分别进行了相关分析。图6以PF4剖面为例,展示了2000年风暴过后,后滨滨面泥沙变化量(黑色粗线)与常浪期水动力要素的时间过程线。从图可见,波高、波陡与后滨单宽泥沙变化量存在明显的负相关性,而平均大潮潮差与后滨单宽泥沙变化量存在一定正相关性。这说明小波高波浪以及大潮均有利于常浪恢复。 图 6 PF4剖面2000年恢复期间后滨泥沙变化量与水动力参数时间过程左轴代表有效波高、波长、波陡、潮位的波动范围,右轴代表后滨单宽泥沙变化量、有效波周期和累积波能Figure 6. Chart of coastal sediment change and dynamic parameters during the recovery period of 2000 of PF4 profileThe left axis represents the fluctuation range of significant wave height, wavelength, wave steepness and tide level, and the right axis represents sediment change of backshore, the significant wave period and the cumulative wave energy
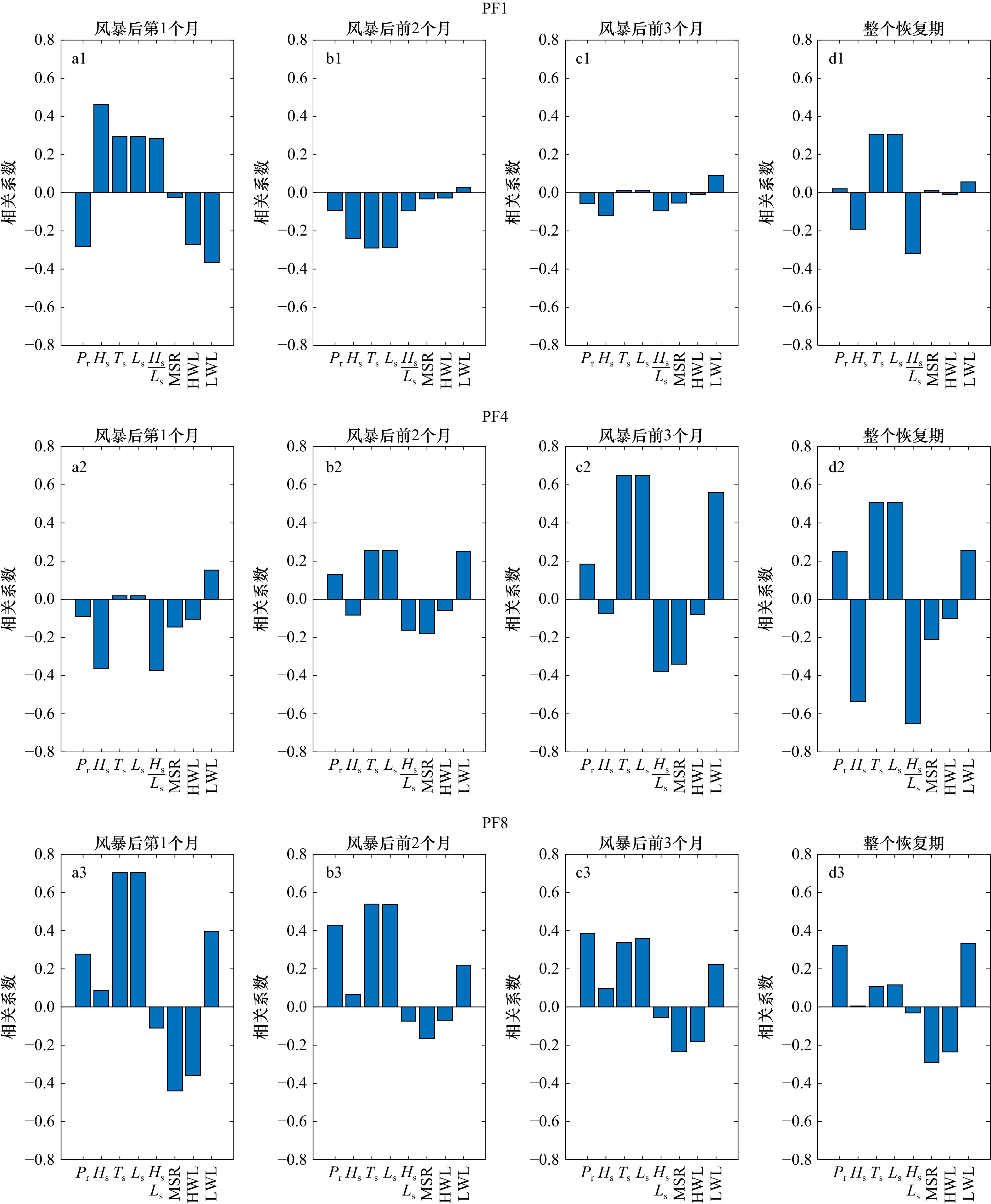
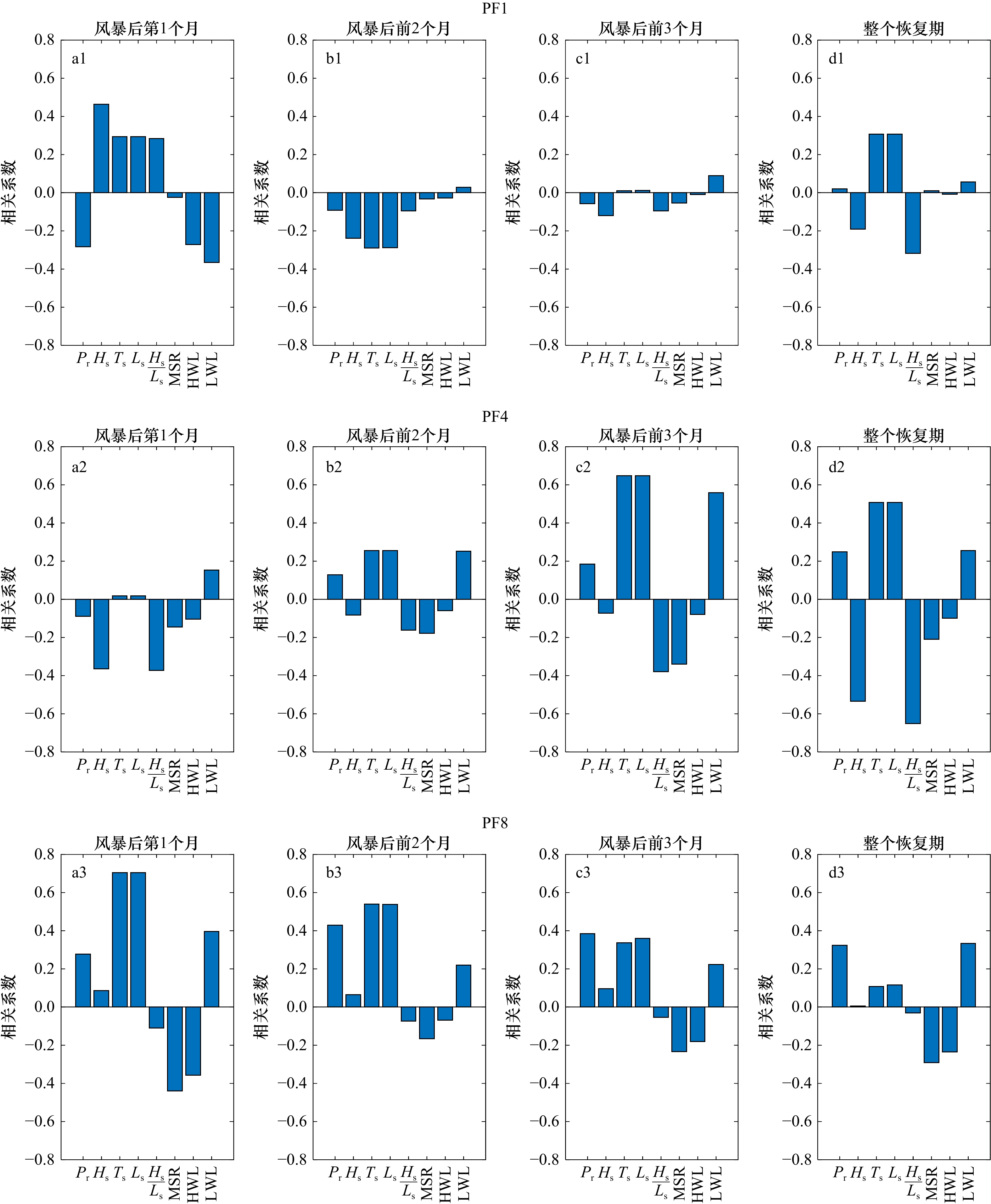
图 6 PF4剖面2000年恢复期间后滨泥沙变化量与水动力参数时间过程左轴代表有效波高、波长、波陡、潮位的波动范围,右轴代表后滨单宽泥沙变化量、有效波周期和累积波能Figure 6. Chart of coastal sediment change and dynamic parameters during the recovery period of 2000 of PF4 profileThe left axis represents the fluctuation range of significant wave height, wavelength, wave steepness and tide level, and the right axis represents sediment change of backshore, the significant wave period and the cumulative wave energy本文综合了不同年份恢复期间的水沙要素,进一步量化了风暴后第1个月(下简称一月期)、风暴后前2个月(下简称二月期)、风暴后前3个月(下简称三月期)以及整个恢复期后滨单宽泥沙变化量与上述水动力要素间的相关系数。由图7可见,对于PF1和PF8剖面,在一月期和二月期内,后滨泥沙变化量和波要素(
$ {H}_{\mathrm{s}} $ 、$ {T}_{\mathrm{s}} $ 、$ {L}_{\mathrm{s}} $ 、$ {H}_{\mathrm{s}}/{L}_{\mathrm{s}} $ )的相关性均较强;在三月期,上述变量间的相关性降低。对于PF4剖面,随着恢复时间的增加,后滨泥沙变化量与波周期($ {T}_{\mathrm{s}} $ )、波长($ {L}_{\mathrm{s}} $ )、波陡($ {H}_{\mathrm{s}}/{L}_{\mathrm{s}} $ )、潮差、潮位等水动力要素的相关性增加。此外,靠近岬角处,波要素对滨面泥沙变化量作用较大,且主要在快速恢复期做功;岬湾处,海滩的恢复在自然力作用下随着时间的推移而持续加强。此外,各剖面的恢复力存在差异。如表1所示,对于北部剖面PF1以及中部剖面PF4,海滩的恢复力与近岸波长(
$ {L}_{\mathrm{s}} $ )正相关,后滨泥沙变化量与$ {L}_{\mathrm{s}} $ 的相关系数(R2)达0.31和0.51;而大波陡的波况抑制海滩的恢复,与后滨泥沙变化量相关性分别为:R2 = –0.31和R2 = –0.65。对于南部沙滩,潮位对于海滩恢复作用逐渐凸显,受到潮控作用的累积波能($ {P}_{\mathrm{r}} $ )对剖面泥沙变化量的影响从北至南依次增大。在南部剖面PF8,$ {P}_{\mathrm{r}} $ 是主要恢复力,与后滨泥沙变化量相关系数达0.34。此外,中部剖面PF4泥沙变化量与各水动力参数的相关性明显大于接近岬头的北部剖面PF1与南部剖面PF8。表 1 各阶段剖面的主要恢复力Table 1. The main restoring power of the profiles at each stage一月期 二月期 三月期 整个恢复期 PF1 有效波高($ {H}_{\mathrm{s}} $) 平均低潮位(LWL) 平均低潮位(LWL) 近岸波长($ {L}_{\mathrm{s}} $) PF4 平均低潮位(LWL) 平均低潮位(LWL) 近岸波长($ {L}_{\mathrm{s}} $) 近岸波长($ {L}_{\mathrm{s}} $) PF8 近岸波长($ {L}_{\mathrm{s}} $) 近岸波长($ {L}_{\mathrm{s}} $) 累积波能($ {P}_{\mathrm{r}} $) 累积波能($ {P}_{\mathrm{r}} $) 5. 讨论
5.1 海岸地貌对常浪恢复的影响
剖面地形对于常浪期的恢复动力和恢复过程均有影响。Wright和Short[16]根据无量纲泥沙参数(
${\varOmega } $ )对海滩剖面进行分类(表2),将海滩剖面分为耗散状态、中间状态和反射状态。根据波浪能量高低,中间状态又可分为沿岸沙坝槽谷(LBT)、韵律沙坝(RBB)、裂流和横向沙坝(TBR)以及低潮台地(LTT)型4种状态,表达式见式(3)和式(4)。Narrabeen海滩大部分沙滩属于中间状态 [6]。$$ \varOmega ={H}_{{\mathrm{b}}}/{\omega }_{{\mathrm{s}}}{T}_{{\mathrm{s}}} \text{,} $$ (3) $$ {\omega }_{{\mathrm{s}}}=\left(Rg{D}^{2}\right)\left/\left[{C}_{1}v+{\left(0.75{C}_{2}Rg{D}^{3}\right)}^{0.5}\right]\right. \text{,} $$ (4) 式中,Hb为破碎波高;
$ {\omega }_{\mathrm{s}} $ 为沉降速度,根据Ferguson和Church[17]提出的公式计算,单位为m/s;$ R $ 为沉积物水下比重,取1.65;$ g=9.8\;\mathrm{m}/{\mathrm{s}}^{2} $ ;$ D $ 为泥沙中值粒径,此处取0.3 mm;$ {C}_{1} $ 、${C}_{2} $ 为常数,Ferguson和Church[17]建议$ {C}_{1}=18 $ 、$ {C}_{2}= 1 $ ;$ v $ 为运动黏滞系数,$ v= 1.0\times{10}^{-6} $ kg·m/s;$ {T}_{\mathrm{s}} $ 为波周期,单位为s;RTR为相对潮差。根据波能分布,PF1剖面属于RBB型[6],所在北部岸段以基岩地貌为主,且有一沙坝潟湖型河口(图8a)。一方面,基岩岬角的存在导致口门外波能辐聚,近岸破碎白帽明显(图8a红圈所示),常浪期也会造成部分冲刷。因而,除快速恢复期外,在常浪期大部分时间,波陡与滨面恢复量负相关(图7)。另一方面,口门外沙坝潟湖的存在为北部岸段提供泥沙来源[18],这解释了快速恢复期,PF1沙丘趾抬升速率和后滨泥沙月均淤积量大于中部和南部剖面(图3)。
PF4剖面属于TRB型(图8b)。Aagaard等[19]曾指出,对于TBR型海滩,沙坝在恢复期不断扩张,沙坝向岸移动的同时挤占裂流通道空间,汇入裂流通道中的泥沙,对于海滩后滨恢复起促进作用。
南部剖面PF8属于LTT型(图8c),一方面,在持续小波作用下,沉积物被不断推送至岸,但随着泥沙淤积,裂流通道泥沙储存能力的降低,泥沙在前滩聚集[20]。另一方面,在波浪和潮流共同作用下,潮间带的沙坝又会向后滨移动[19]。由此,波浪对后滨泥沙的输送作用减小,而潮汐对后滨泥沙运移的控制作用增强,因而
$ {P}_{\mathrm{r}} $ 在PF8的常浪恢复过程中起主要作用(图7)。戚洪帅等[21]在研究华南海滩动力地貌特征时发现,对于LTT型海滩,高潮位时水深增加使得激浪带范围减小,进而导致能量耗散减小、波能更加集中,并对滩面的上部分造成更强烈的侵蚀。上述发现与Narrabeen南部剖面PF8在恢复期受到更强的潮控作用,且高潮位(HWL)对此处风暴剖面的恢复起抑制作用相符。自从2011年起,新南威尔士大学(UNSW)测量并公开了Narrabeen海滩剖面一部分潮下带地形数据。该岬湾沙滩的剖面地形测深数据2012年为例显示(图9):从北至南的3个剖面潮下带地质与地形均差异较大。其中,北部PF1剖面在8~10 m等深线间有一段平坡,9 m水深以下为基岩;中部PF4剖面呈抛物线型,水下也为砂质底层;PF8剖面由于靠近南端岬角,其水深在5 m处也为基岩。潮下带地质地貌影响着常浪期的恢复过程和恢复动力。以砂质基地为特征的PF4剖面受波浪、潮动力作用,泥沙更快地向后滨滨面输送,因而,图7中水动力要素与滨面恢复量的相关性较剖面PF1与PF8更强,此外,这一解释也与PF4所处岸段在常浪期岸线向海前进速度最快的现象相符。
综上,岬湾海滩各剖面由于所处岸段地质地貌不同,影响了水动力环境,如波浪爬高、水流冲越等,因而表现出恢复过程、恢复动力的沿岸差异性,这也部分解释了图4中沙丘趾位置沿岸分布的曲折特点。
5.2 南方涛动指数与海滩剖面动力地貌之间的关系
在年际时间尺度上,南方涛动(ENSO)会对澳洲的波浪气候产生强烈影响[22]。Short等[23]发现Narrabeen海滩旋转的年际规律与南方涛动指数(SOI)存在一定关联:在厄尔尼诺期间,海滩北端淤积,而南端侵蚀,导致海滩的净顺时针旋转;拉尼娜阶段发生相反的情况,海滩逆时针旋转。Ranasinhe等[24]随后阐述了SOI与波浪气候、海滩旋转之间的明确联系,拉尼娜现象期间东北方向的波浪增多,这些波浪沿着整个海滩斜向入射,导致向南的沿岸流,而南部岬角的存在导致海滩中北部被沿岸流侵蚀的泥沙沉积在海滩南端。在之后的研究中,笔者通过不同于Short所用时段的数据验证了这一现象[4]。之后的研究发现Narrabeen海滩南部的Moruay海滩和Pedro海滩,与之存在同步旋转行为,波能较低的海滩旋转程度加剧[25]。值得注意的是,这类海滩旋转具有普适性。在法国北布列塔尼Vougot海滩同样发现了岸线的旋转现象[26]。研究指出,Vougot海滩在特定年份东部易感风暴浪,当叠加高潮位时,岸线和沙丘趾后退显著,泥沙向西流动,在西部沙滩的淤积,从而造成了海滩旋转。本研究则发现海滩的旋转特性与ENSO对于各剖面的恢复动力起到调制作用相关。
图10比较了恢复期间水动力要素、后滨泥沙恢复量、南方涛动指数(SOI)的时间过程。其中,SOI指数为负(正)代表趋于厄尔尼诺现象(拉尼娜现象),太平洋赤道附近海水表现出异常高(低)温度。例如,1997年是典型的厄尔尼诺年,而1998–2000年期间则发生了持久且强烈的拉尼娜现象。研究发现,拉尼娜期间,风暴剖面的恢复能力减弱,具体表现为:对于北部剖面PF1以及中部剖面PF4,波陡与后滨泥沙恢复量的负相关性在增强(PF1:R2 = –0.41, PF4:R2 = –0.85);而对于南部剖面PF8,平均高潮位与后滨泥沙恢复量的负相关性更加明显(R2 = –0.47)。拉尼娜现象期间,北部波陡与滨面泥沙变化量的强相关性也从侧面揭示了为何北部沙滩更易侵蚀且不易恢复,受侵蚀后泥沙顺岸流动,在南部岸段淤积,从而形成海滩的逆时针旋转现象。
此外,结合图3中后滨泥沙变化量过程线,强拉尼娜盛行期间(1998年、2000年、2011年),相较于弱拉尼娜现象期间(1995年、2012年)风暴恢复过程明显较长。厄尔尼诺期间(1997年)风暴浪恢复过程远长于其他年份,这主要由于1997年的风暴浪强度远大于其他5起事件(图1d)。Karunarathna等[27]发现风暴强度增加,海滩的侵蚀程度加剧。可见,风暴强度对于海滩的恢复能力起到主导作用。
6. 结论
Narrabeen海滩30年间经历了交替发生的风暴侵蚀和常浪恢复过程,海滩在鲜有人工干预的情况下,呈现出沙坝剖面和滩肩剖面交替出现的特性。为探明岬湾海滩在经历风暴浪后的自恢复能力,本文通过大量实测数据分析了典型风暴浪过后,后滨滨面泥沙变化的主要动力要素,得到以下主要结论:
(1)岬角处,波浪、潮汐等动力因素对滨面泥沙恢复量短期(首月)影响较大,而在岬湾处滨面泥沙变化量对水动力的响应随着恢复时间增加而持续;该空间差异与剖面所在位置处波高、波向、地貌形态、地质条件均相关。
(2)北部PF1及中部PF4风暴剖面在常浪期的恢复过程主要受到小波高波浪作用,而对于南部剖面PF8,潮控作用在增强;本文提出了考虑潮差影响的累积波能概念(
$ {P}_{{\mathrm{r}}} $ ),在水动力较复杂的南部剖面PF8,其恢复能力与$ {P}_{{\mathrm{r}}} $ 正相关。(3)风暴剖面的恢复能力还受到南方涛动指数的影响,在拉尼娜现象盛行期间,海滩剖面的恢复能力普遍减弱,波陡增加和高潮位频发抑制了风暴剖面的恢复,受地形影响存在南北差异 ,后者造成了岸线整体态势发生旋转。
-
图 3 典型风暴事件过后在恢复期的后滨滨面逐月泥沙量时间过程线(a);不同恢复期内,各剖面岸线月均向海前进量与沙丘趾月均抬升量的相对变化对比(b)
Fig. 3 Time series of the monthly-mean sediment volume on the backshore during the recovery period after each typical storm event (a); comparison of the ratios of the monthly-averaged seaward displacement of the shoreline’s position over the monthly-averaged elevated displacement of the dune toe for each profile during different recovery periods (b)
图 6 PF4剖面2000年恢复期间后滨泥沙变化量与水动力参数时间过程
左轴代表有效波高、波长、波陡、潮位的波动范围,右轴代表后滨单宽泥沙变化量、有效波周期和累积波能
Fig. 6 Chart of coastal sediment change and dynamic parameters during the recovery period of 2000 of PF4 profile
The left axis represents the fluctuation range of significant wave height, wavelength, wave steepness and tide level, and the right axis represents sediment change of backshore, the significant wave period and the cumulative wave energy
表 1 各阶段剖面的主要恢复力
Tab. 1 The main restoring power of the profiles at each stage
一月期 二月期 三月期 整个恢复期 PF1 有效波高($ {H}_{\mathrm{s}} $) 平均低潮位(LWL) 平均低潮位(LWL) 近岸波长($ {L}_{\mathrm{s}} $) PF4 平均低潮位(LWL) 平均低潮位(LWL) 近岸波长($ {L}_{\mathrm{s}} $) 近岸波长($ {L}_{\mathrm{s}} $) PF8 近岸波长($ {L}_{\mathrm{s}} $) 近岸波长($ {L}_{\mathrm{s}} $) 累积波能($ {P}_{\mathrm{r}} $) 累积波能($ {P}_{\mathrm{r}} $) -
[1] Zhou Yingtao, Feng Xi, Liu Maoyuan, et al. Influence of beach erosion during wave action in designed artificial sandy beach using XBeach model: profiles and shoreline[J]. Journal of Marine Science and Engineering, 2023, 11(5): 984. doi: 10.3390/jmse11050984 [2] 战超. 莱州湾东岸岬间海湾海岸地貌演变过程与影响机制[D]. 烟台: 中国科学院烟台海岸带研究所, 2017.Zhan Chao. Evolution of coastal geomorphology and influence mechanism of headland bay along eastern Laizhou Bay[D]. Yantai: Yantai Institution of Coastal Zone Research Chinese Academy of Sciences, 2017. [3] 冯曦, 易风, 曹海锦, 等. 南黄海辐射沙洲近岸海域波浪特性研究[J]. 海洋工程, 2018, 36(1): 62−73.Feng Xi, Yi Feng, Cao Haijin, et al. An observational study on wave characteristics at the Jiangsu Radial Sand Ridges in the South Yellow Sea of China[J]. The Ocean Engineering, 2018, 36(1): 62−73. [4] 周嬴涛, 冯曦, 管卫兵, 等. 波浪作用下岬湾海滩蚀积特点: 以澳大利亚Narrabeen海滩为例[J]. 科学通报, 2019, 64(2): 223−233. doi: 10.1360/N972018-00376Zhou Yingtao, Feng Xi, Guan Weibing, et al. Characteristics of beach erosion in headland bays due to wave action: taking the Narrabeen Beach in Australia as an example[J]. Chinese Science Bulletin, 2019, 64(2): 223−233. doi: 10.1360/N972018-00376 [5] Phillips M S, Harley M D, Turner I L, et al. Shoreline recovery on wave-dominated sandy coastlines: the role of sandbar morphodynamics and nearshore wave parameters[J]. Marine Geology, 2017, 385: 146−159. doi: 10.1016/j.margeo.2017.01.005 [6] Turner I L, Harley M D, Short A D, et al. A multi-decade dataset of monthly beach profile surveys and inshore wave forcing at Narrabeen, Australia[J]. Scientific Data, 2016, 3(1): 160024. doi: 10.1038/sdata.2016.24 [7] Bennett W G, Karunarathna H, Reeve D E, et al. Computational modelling of morphodynamic response of a macro-tidal beach to future climate variabilities[J]. Marine Geology, 2019, 415: 105960. doi: 10.1016/j.margeo.2019.105960 [8] Lord D, Kulmar M. The 1974 storms revisited: 25 years experience in ocean wave measurement along the South-East Australian coast[C]//Proceedings of the 27th International Conference on Coastal Engineering. Sydney: ASCE, 2001. [9] Harley M, D Turner I L, Short A D, et al. An empirical model of beach response to storms-SE Australia[C]//Proceedings of the 19th Australasian Conference on Coastal and Ocean Engineering. Wellington: Engineers Australia, 2009. [10] Short A D, Trenaman N L. Wave climate of the Sydney region, an energetic and highly variable ocean wave regime[J]. Australian Journal of Marine and Freshwater Research, 1992, 43(4): 765−791. doi: 10.1071/MF9920765 [11] Davidson M A, Turner I L, Splinter K D, et al. Annual prediction of shoreline erosion and subsequent recovery[J]. Coastal Engineering, 2017, 130: 14−25. doi: 10.1016/j.coastaleng.2017.09.008 [12] Phillips M S, Turner I L, Cox R J, et al. Will the sand come back? Observations and characteristics of beach recovery[C]//Proceedings of the Australasian Coasts & Ports Conference 2015. Auckland: Engineers Australia and IPENZ, 2015. [13] Dolan R, Davies R E. Coastal storm hazards[J]. Journal of Coastal Research, 1994: 103−114. [14] Davis R A, Fox W T, Hayes M O, et al. Comparison of ridge and runnel systems in tidal and non-tidal environments[J]. Journal of Sedimentary Petrology, 1972, 42(2): 413−421. [15] 冯曦, 江沅书, 周嬴涛, 等. 常浪期沙质海滩风暴剖面自然恢复过程研究[J]. 泥沙研究, 2023, 48(1): 57−64.Feng Xi, Jiang Yuanshu, Zhou Yingtao, et al. Study on the natural restoration processes of beach storm-profile[J]. Journal of Sediment Research, 2013, 48(1): 57−64. [16] Wright L D, Short A D. Morphodynamic variability of surf zones and beaches: a synthesis[J]. Marine Geology, 1984, 56(1/4): 92−118. [17] Ferguson R I, Church M. A simple universal equation for grain settling velocity[J]. Journal of Sedimentary Research, 2004, 74(6): 933−937. doi: 10.1306/051204740933 [18] Woodroffe C D. Coast, Form, Process and Evolution[M]. Cambridge: Cambridge University Press, 2002. [19] Aagaard T, Greenwood B, Hughes M. Sediment transport on dissipative, intermediate and reflective beaches[J]. Earth-Science Reviews, 2013, 124: 32−50. doi: 10.1016/j.earscirev.2013.05.002 [20] Hine A C. Mechanisms of berm development and resulting beach growth along a barrier spit complex[J]. Sedimentology, 1979, 26(3): 333−351. doi: 10.1111/j.1365-3091.1979.tb00913.x [21] 戚洪帅, 蔡锋, 雷刚, 等. 华南海滩风暴响应特征研究[J]. 自然科学进展, 2009, 19(9): 975−985.Qi Hongshuai, Cai Feng, Lei Gang, et al. The response characteristics of beaches to tropical storms in South China[J]. Progress in Natural Science, 2009, 19(9): 975−985. [22] Andrews E D, Antweiler R C, Neiman P J, et al. Influence of ENSO on flood frequency along the California coast[J]. Journal of Climate, 2004, 17(2): 337−348. doi: 10.1175/1520-0442(2004)017<0337:IOEOFF>2.0.CO;2 [23] Short A D, Trembanis A C, Turner I L. Beach oscillation, rotation and the southern oscillation, Narrabeen Beach, Australia[C]//Proceedings of the 27th International Conference on Coastal Engineering. Sydney: ASCE, 2001: 2439−2452. [24] Ranasinghe R, McLoughlin R, Short A, et al. The Southern Oscillation Index, wave climate, and Beach rotation[J]. Marine Geology, 2004, 204(3/4): 273−287. [25] Short A D, Bracs M A, Turner I L. Beach oscillation and rotation: local and regional response at three beaches in Southeast Australia[J]. Journal of Coastal Research, 2014, 70(10070): 712−717. [26] Suanez S, Yates M L, Floc’h F, et al. Using 17 years of beach/dune profile monitoring to characterize morphological dynamics related to significant extreme water level events in North Brittany (France)[J]. Geomorphology, 2023, 433: 108709. doi: 10.1016/j.geomorph.2023.108709 [27] Karunarathna H, Pender D, Ranasinghe R, et al. The effects of storm clustering on beach profile variability[J]. Marine Geology, 2014, 348: 103−112. doi: 10.1016/j.margeo.2013.12.007 -






 下载:
下载:
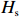
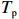
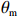
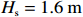
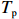
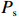
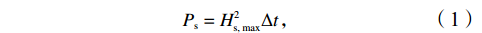
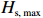
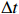
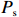



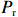
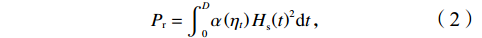
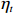
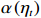
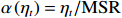
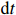
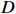
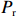
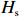
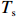
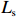
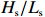
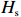
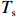
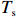
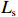
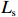
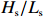
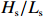

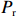
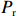
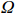
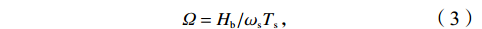
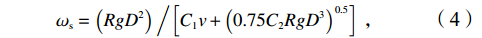
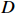
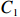
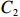
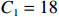
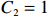
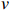
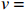
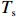

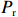


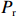
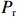

 下载:
下载: