Summary for “Liquefaction stabilization of the seabed around a sloping breakwater under bimodal spectral waves”
-
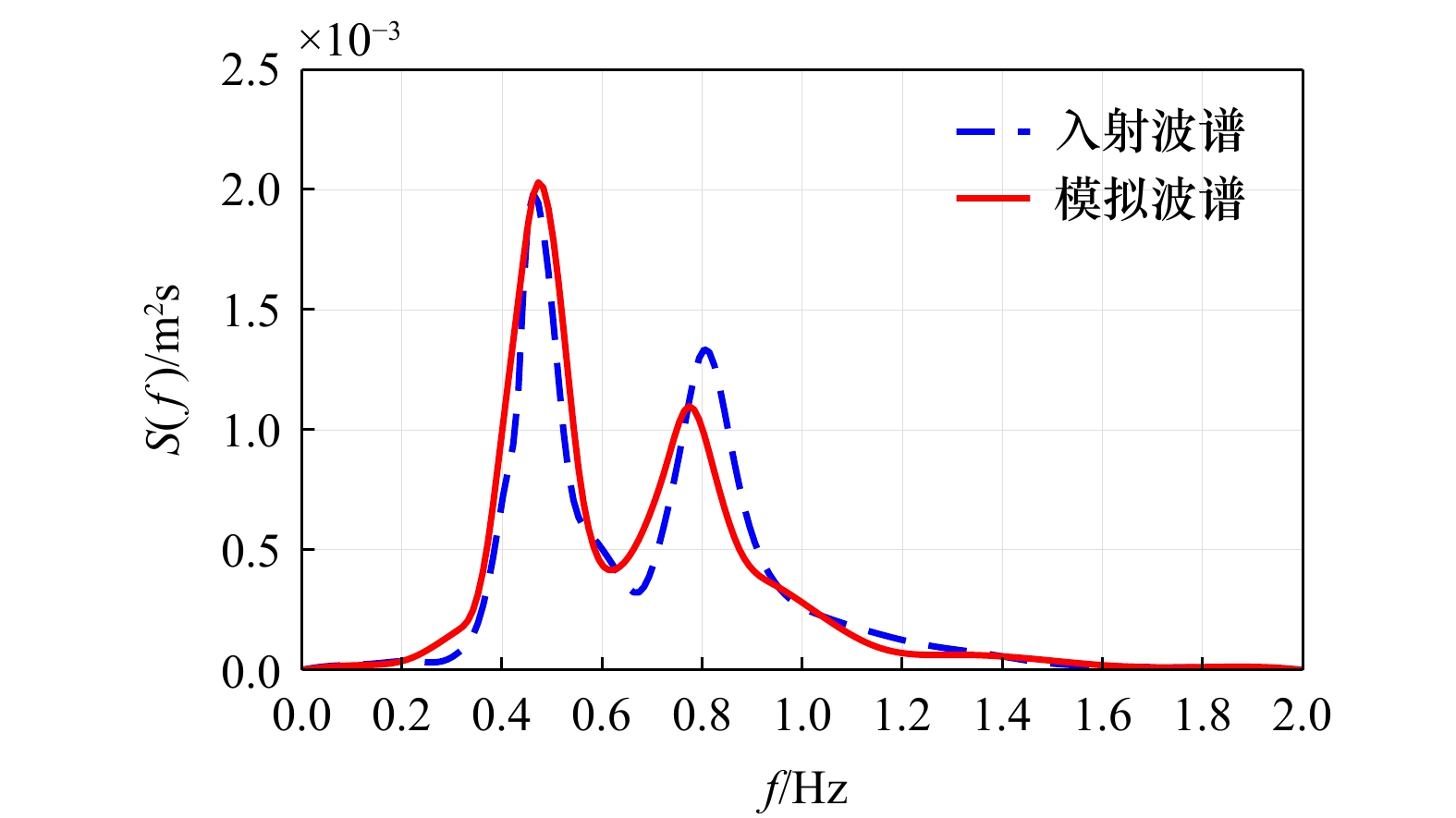
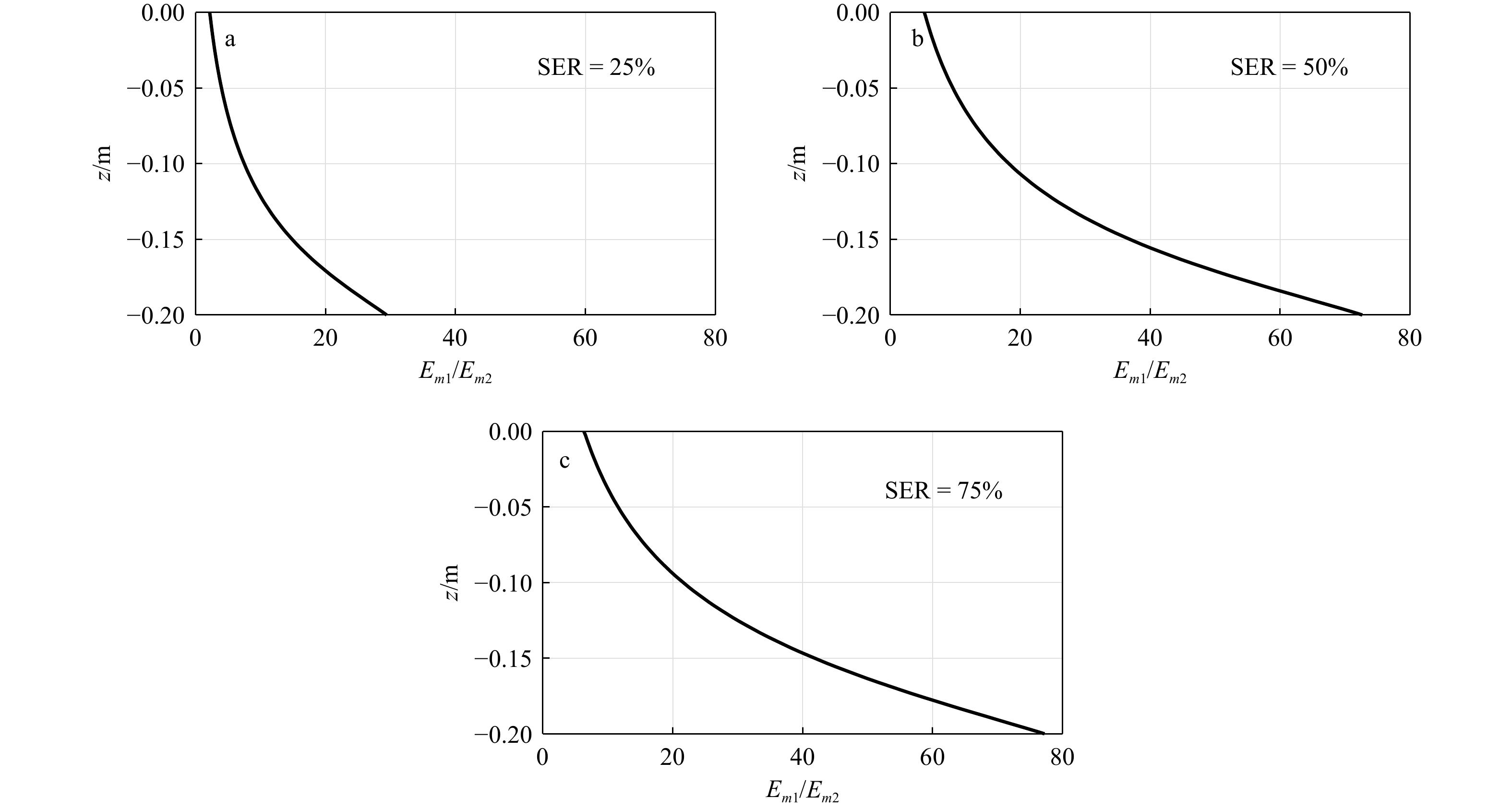
摘要: 西非海域受到北大西洋远程涌浪的影响，形成了独特的双峰波浪现象，这对防波堤的设计与稳定性构成了挑战。本文建立了一个基于雷诺时均的Navier-Stokes方程和k-ω湍流模型的数值波浪水槽，耦合了基于Biot半动态（u-p假设）多孔弹性介质理论的海床模块与结构物模块，数值模拟并研究了双峰谱随机波浪−斜坡式防波堤−海床相互作用机制。基于Soares四参数法构造的双峰谱随机波浪荷载动力条件，本文分析了斜坡式防波堤前的水动力特征，探讨了斜坡堤周围海床的动力响应、液化的时空分布规律及频域特征，阐明了不同双峰谱涌浪能量占比对海床孔压分布及液化特性的影响。结果表明，随着双峰谱涌浪占比的增加，海床内低频孔压越来越显著，且更加容易穿透海床向海床深度传播。在海床液化显著区域，液化深度随着双峰谱波浪中涌浪占比的增加而增大，且高频和低频孔压对海床液化的影响程度随着距离防波堤堤脚位置的增加交替上升。本研究为斜坡式防波堤的设计与基础稳定评估提供科学依据。Abstract: This article explores the distinctive marine environment of the West African coastal region, with a particular focus on bimodal waves-induced seabed response and stability around sloping breakwaters. Bimodal waves are a unique wave pattern observed in the West African Sea, influenced by distant swells from the North Atlantic. These waves present new challenges in marine engineering, particularly in the design and maintenance of breakwater structures. A complex numerical model has been developed to simulate the interaction between bimodal spectrum random waves and sloping breakwaters. This model is grounded in the Reynolds-averaged Navier-Stokes equations and employs the k-ω turbulence model to simulate the flow field and pressure distribution around the breakwater. Furthermore, the model incorporates Biot’s semi-dynamic porous medium theory (the u-p model) to assess wave-induced pore pressure and the liquefaction features of the seabed. The study found that the pore pressure response varies under different conditions, generally indicating that pore pressure increases with the swell energy ratio (SER). It was observed that low-frequency pore pressure becomes more pronounced with increasing depth and swell wave ratio. Analyzing the swell energy ratio revealed that the attenuation rate of low-frequency energy is lower than that of high-frequency energy. As the swell energy ratio increases, the pore pressure response in the seabed intensifies significantly, leading to an expansion in the range and depth of seabed liquefaction, especially noticeable at certain distances in front of the breakwater. Furthermore, the influence of high-frequency and low-frequency pore pressure on seabed liquefaction alternates with the increasing distance from the breakwater’s toe. This study provides a scientific basis for the design and stability assessment of sloping breakwaters.
-
Key words:
- bimodal waves /
- sloping breakwater /
- seabed liquefaction /
- numerical simulation
-
图 2 数值模拟与物理模型试验波面对比
Fig. 2 Numerical simulation and physical model test wave face comparison
图 3 数值模拟与物理模型试验孔压对比
Fig. 3 Numerical simulation and physical model test pore pressure comparison.
图 5 不同深度处随机波致孔压时间序列及频谱图（SER=0%、50%）
Fig. 5 Time series and spectrogram of random wave pore pressure at different depths（SER=0%、50%）
图 6 谱峰能量比值沿深度方向变化
Fig. 6 Variation of the spectral peak energy ratio along the depth direction.
图 8 风涌浪占比与高低频孔压对最大液化范围与深度的影响（点线：低频；虚线：高频）
Fig. 8 Effect of SER and high/low frequency pore pressure on the maximum liquefaction range and depth. (dot line: low frequency; dashed line: high frequency)
表 1 海床参数
Tab. 1 Seabed parameters
海床参数 符号 值 单位 杨氏模量 E 100 Mpa 泊松比 μ 0.33 / 剪切模量 G 37.6 Mpa 渗透系数 K 0.0001 m/s 土体饱和度 Sr 0.98 / 孔隙率 n 0.3 / 密度 ρs 2650 kg/m3 
下载: 导出CSV
-
[1] 朱建, 窦培林, 陈刚, 等. 西非海域涌浪对多点系泊FPSO水动力性能影响分析[J]. 中国造船, 2014, 55(3): 117−124 doi: 10.3969/j.issn.1000-4882.2014.03.013Zhu Jian, Dou Peilin, Chen Gang, et al. Influence of swell on hydrodynamic performances of FPSO in West Africa waters[J]. Shipbuilding of China, 2014, 55(3): 117−124. doi: 10.3969/j.issn.1000-4882.2014.03.013 [2] Nerzic R, Frelin C, Prevosto M, et al. Joint distributions of wind/waves/current in West Africa and derivation of multivariate extreme I-FORM contours[C]//The Seventeenth International Offshore and Polar Engineering Conference. Lisbon: ISOPE, 2007: ISOPE-I-07-298. [3] Orimoloye S, Horrillo-Caraballo J, Karunarathna H, et al. Wave overtopping of smooth impermeable seawalls under unidirectional bimodal sea conditions[J]. Coastal Engineering, 2021, 165: 103792. doi: 10.1016/j.coastaleng.2020.103792 [4] 王野, 温鸿杰, 余锡平. 波浪作用下抛石基床上沉箱稳定性的SPH模拟[J]. 科学通报, 2021, 66(36): 4700−4708 doi: 10.1360/TB-2021-0914Wang Ye, Wen Hongjie, Yu Xiping. SPH modeling of caisson stability on rubble-mound foundation under wave action[J]. Chinese Science Bulletin, 2021, 66(36): 4700−4708. doi: 10.1360/TB-2021-0914 [5] Guo L, Qu K, Wang X, et al. Numerical study on performance of submerged permeable breakwater under impacts of multi-directional focused wave groups[J]. Ocean Engineering, 2024, 302: 117665. doi: 10.1016/j.oceaneng.2024.117665 [6] Zhao Enjin, Dong Youkou, Tang Yuezhao. Performance of submerged semi-circular breakwater under solitary wave in consideration of porous media[J]. Ocean Engineering, 2021, 223: 108573. doi: 10.1016/j.oceaneng.2021.108573 [7] Chen Mili, Yan Shichang, Yang Yue, et al. Experimental study on wave height distribution outside harbor for composite rubble mound breakwaters[J]. China Harbour Engineering, 2022, 42(1): 45−47. (查阅网上资料, 本条文献为中文文献, 请确认) [8] Putnam J A. Loss of wave energy due to percolation in a permeable sea bottom[J]. Eos, Transactions American Geophysical Union, 1949, 30(3): 349−356. doi: 10.1029/TR030i003p00349 [9] Yamamoto T, Koning H L, Sellmeijer H, et al. Discrete element numerical simulation of the accumulation process of wave-induced pore water pressure in the seabed[J]. Haiyang Xuebao, 1978, 87: 193−206. (查阅网上资料, 未找到本条文献信息, 请确认) [10] Madsen O S. Wave-induced pore pressures and effective stresses in a porous bed[J]. Géotechnique, 1978, 28(4): 377−393. [11] Zienkiewicz O C, Chang C T, Bettess P. Drained, undrained, consolidating and dynamic behaviour assumptions in soils[J]. Géotechnique, 1980, 30(4): 385−395. [12] Hsu J R C, Jeng D S. Wave-induced soil response in an unsaturated anisotropic seabed of finite thickness[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1994, 18(11): 785−807. doi: 10.1002/nag.1610181104 [13] Tsai C P, Lee T L. Standing wave induced pore pressures in a porous seabed[J]. Ocean Engineering, 1995, 22(6): 505−517. doi: 10.1016/0029-8018(95)00003-4 [14] 王岳, 刘春, 刘晓磊, 等. 波浪作用下海床孔压累积过程离散元数值模拟[J]. 海洋学报, 2021, 43(11): 88−95Wang Yue, Liu Chun, Liu Xiaolei, et al. Discrete element numerical simulation of the accumulation process of wave-induced pore water pressure in the seabed[J]. Haiyang Xuebao, 2021, 43(11): 88−95. [15] 倪云林, 龚倩, 沈梦佳. 渗透海床上矩形Bragg防波堤对波浪反射的研究[J]. 海洋学报, 2022, 44(9): 124−131 doi: 10.12284/j.issn.0253-4193.2022.9.hyxb202209011Ni Yunlin, Gong Qian, Shen Mengjia. Study of wave reflection by the Bragg breakwater with rectangular bars on the permeable seabed[J]. Haiyang Xuebao, 2022, 44(9): 124−131. doi: 10.12284/j.issn.0253-4193.2022.9.hyxb202209011 [16] Ye Jianhong, Shan Jipeng, Zhou Haoran, et al. Numerical modelling of the wave interaction with revetment breakwater built on reclaimed coral reef islands in the South China Sea-experimental verification[J]. Ocean Engineering, 2021, 235: 109325. doi: 10.1016/j.oceaneng.2021.109325 [17] Li Zhengxu, Jeng D S. Dynamic soil response around two-layered detached breakwaters: three-dimensional OpenFOAM model[J]. Ocean Engineering, 2023, 268: 113582. doi: 10.1016/j.oceaneng.2022.113582 [18] Duan Lunliang, Wang Duoyin. Novel three-dimensional numerical model for residual seabed response to natural loadings near a single pile[J]. Applied Ocean Research, 2020, 94: 102004. doi: 10.1016/j.apor.2019.102004 [19] Ochi M K, Hubble E N. Six-parameter wave spectra[C]//Coastal Engineering Proceedings. 1976: 301−328. (查阅网上资料, 未找到本条文献出版信息, 请确认) [20] Soares C G. Representation of double-peaked sea wave spectra[J]. Ocean Engineering, 1984, 11(2): 185−207. doi: 10.1016/0029-8018(84)90019-2 [21] Jonah F E. Managing coastal erosion hotspots along the Elmina, Cape Coast and Moree area of Ghana[J]. Ocean & Coastal Management, 2015, 109: 9−16. [22] Luth H R, Klopman G, Kitou N. Kinematics of waves breaking partially on an offshore bar, LVD measurements for waves without a net onshore current[R]. Delft, the Netherlands: Delft Hydraulics, 1994. [23] 卢海斌. 波浪作用下沙质海床孔隙水压力的研究[D]. 长沙: 长沙理工大学, 2005Lu Haibin. The research on pore water pressure response to waves in sandy seabed[D]. Changsha: Changsha University of Science & Technology, 2005. [24] Kim I C, Kaihatu J M. A modified frequency distribution function of wave-breaking-induced energy dissipation[J]. Journal of Geophysical Research: Oceans, 2022, 127(12): e2022JC018792. doi: 10.1029/2022JC018792 [25] Zen K, Yamazaki H. Oscillatory pore pressure and liquefaction in seabed induced by ocean waves[J]. Soils and Foundations, 1990, 30(4): 147−161. doi: 10.3208/sandf1972.30.4_147 [26] Jeng D S. Wave-induced seabed instability in front of a breakwater[J]. Ocean Engineering, 1997, 24(10): 887−917. doi: 10.1016/S0029-8018(96)00046-7 -
图(8) / 表(1)
计量
- 文章访问数: 60
- HTML全文浏览量: 32
- PDF下载量: 9
- 被引次数: 0
