Simulation of a jet under the combined action of waves and currents using a momentum integral model
-
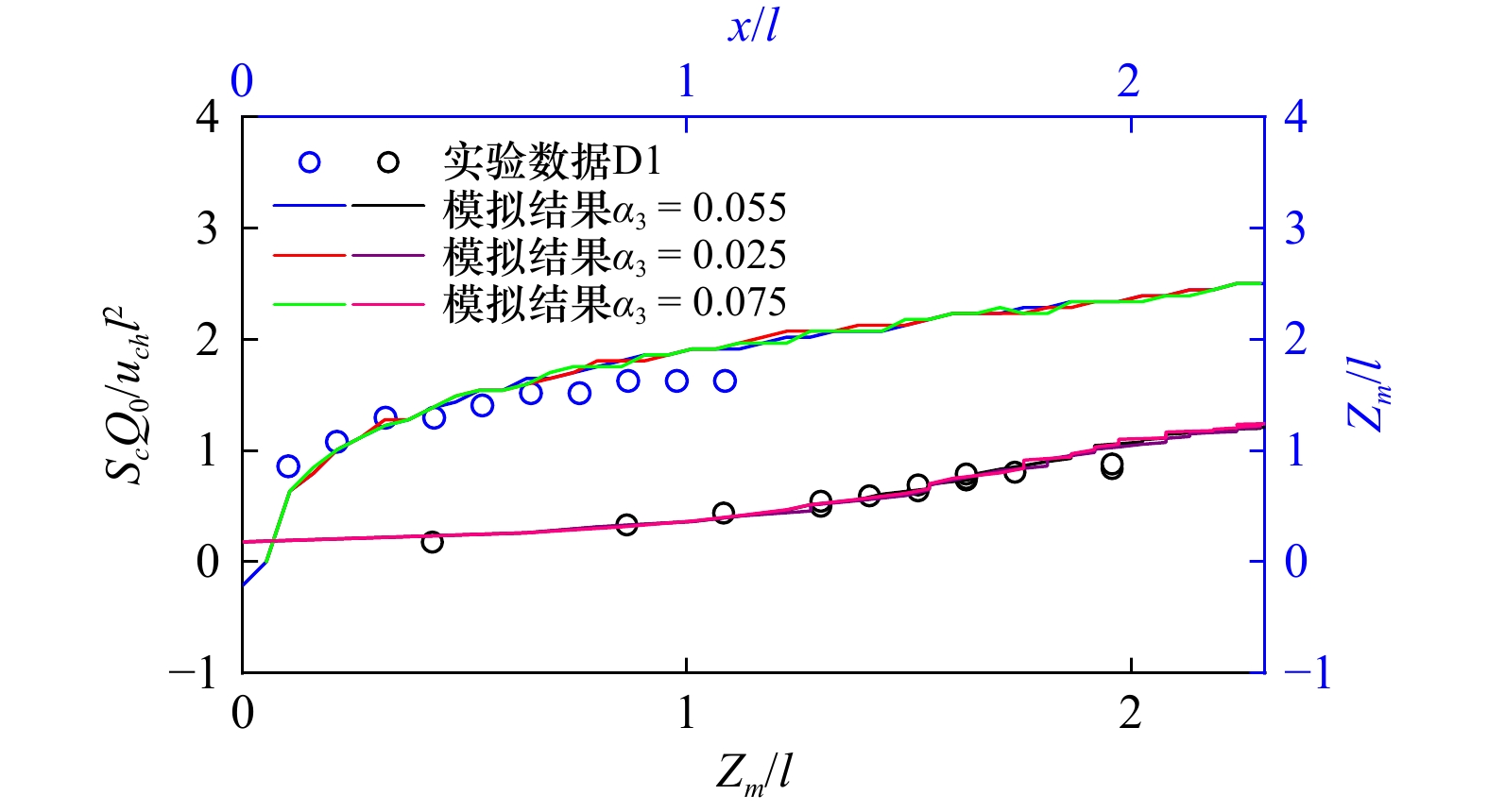
摘要: 污水通常以射流的形式向海排放，其在海洋环境水体中的稀释过程是射流与波浪、潮流共同作用的结果。本文基于合理的假设条件，对射流运动的控制方程进行积分处理，结合波流环境下射流的结构特征，引入射流卷吸与拖曳力函数，结合必要的边界条件，形成封闭的控制方程组，建立波流环境下射流动量积分模型。通过与实验资料的对比分析可以看出，该模型可以准确模拟波流环境下射流在近区段的时均运动与稀释过程；相较于单一的横流作用，波流共同作用下射流对周边水体的影响范围更大，射流初始稀释能力更强。基于多个组次的动量积分模拟实验，通过无量纲分析与最小二乘拟合，建立了波流共同作用下射流轨迹中心线位置及最小稀释度的经验公式。相关成果可为排海污水环境影响评估提供快速、准确的分析手段。Abstract: Wastewater is usually discharged into the sea in the form of jet, and its dilution process is the result of the interaction of jet, wave and tidal current. In this study, based on the reasonable assumptions, the governing equations are integrated to the form of ordinary differential equations. According to the hydrodynamic characteristics of the jet in the wavy current environment, the entrainment and drag force functions of the jet are introduced to close the governing equations, thus the integral model for the turbulent jet under the combined action of waves and currents is established. Through comparison and verification, it is confirmed that the integral model can accurately simulate the time average movement and dilution process of the near-field jet under the wavy current environment. It is found that compared with a pure current environment, the influence range of jet on the surrounding water is larger than that in a wavy current environment, and the dilution capacity of jet can be remarkably enhanced by the wave effect. Based on the momentum integral simulation results, the empirical fitting formulas for the position of the jet cross-sectional trajectory line and the minimum dilution in the wavy current environment are established. The developed model could be served as an efficient and accurate tool to assess the environmental impacts of submarine outfalls on the surrounding waters.
-
1. 引言
污水向海排放是沿海地区典型的污水处理方式之一[1]。污水从排放口进入环境水体，并与其发生强烈掺混形成排海污水射流，在波浪和潮流的共同作用下进行扩散稀释，对环境水体产生影响。因此，开展波流共同作用下射流运动与稀释研究对于科学评价污水向海排放工程的环境影响有着重要的现实意义。
射流在环境水体动力的作用下主要分为近区快速稀释和远区随流扩散两个发展阶段[2]。射流在近区段，受自身动力影响不断卷吸周围水体，速度逐渐减小，污染物浓度得到快速稀释；射流在远区段，主要与环境水体一起随流扩散，稀释程度逐渐降低。本文重点研究的是射流在近区段的运动与稀释过程。考虑到潮流的时间尺度相较于射流的时间尺度要长得多，可以将潮流对射流的影响近似看成一系列恒定水流对射流的影响，而波浪的时间尺度与射流的时间尺度相当，波浪水质点的来回摆动对射流的发展将起到较强的制约作用[3]。
针对单一水流或波浪作用下的射流运动与稀释特性，国内外已经开展了大量物理实验与数值模拟研究。姜国强和李炜[4]及姜国强等[5]采用粒子图像测速（PIV）系统对动水环境下多种喷口长度和流速比情况下的有限宽窄缝紊动射流近区流场进行测试，并结合数值模拟结果分析讨论了射流的旋涡结构与近区三维流动特性。周丰等[6]使用PIV系统对有限水深规则波浪环境下圆形垂直射流进行了实验研究，分析了波周期对射流的影响，结果表明波周期对射流的流场特性有一定的影响。Anghan等[7]详细分析了规则波和随机波对射流速度衰减系数、射流宽度和轴向速度分布等平均特性以及轴向、侧向紊动强度和雷诺剪应力的影响。与静水射流相比，波浪引起的水质点摆动使得射流与周边水体的掺混和卷吸明显增大，射流的稀释度明显提高，射流的紊动强度也显著增大[8]。
针对波浪与水流共同作用下射流在近区段的运动与稀释特性，国内外学者也取得了不少的研究成果。Abdel-Rahman和Eleshaky[9]对波流环境下垂直向下射流的时均和紊动特性进行物理实验研究，发现相较于单一横流作用，射流的初始稀释得到增强。袁丽蓉等[10]用各向异性k-ε紊流模型和VOF方法对波流环境下的垂向窄缝紊动射流作了模拟，分析了波流环境下波浪周期和波高对浓度场分布的影响。鲁俊等[11]利用大涡数学模型对波流共同作用下二维窄缝射流进行了数值模拟，分析了波流对于射流轨迹的影响。王娅娜[12]采用PIV和PLIF技术对波浪和水流共同作用下垂向射流进行研究，发现了波流环境下射流的“水团”现象，并基于瞬时射流比阐述了其形成机理，通过实验数据的拟合建立了射流运动轨迹、轴线速度和稀释度等的无量纲经验公式。Xu等[13–15]利用物理实验与大涡数学模型进行了对比验证，利用新定义的特征长度拟合得到了描述波流环境下射流三维运动轨迹中心及相应位置稀释度的无量纲经验公式。
相较于以往常用的基于偏微分方程的数值模拟方法，动量积分模拟法可以通过对控制方程的简化，沿射流行进方向断面进行数值积分，得到射流运动方程的常微分形式，从而实现射流时均速度场和浓度场的快速计算，在工程计算中有很好的应用价值。Chin[16]开发了一个动量积分模型来模拟波浪环境中动量射流和浮力射流的运动情形，但仅采用了射流到达表面时的稀释度实验数据对模型进行了验证，因此具有一定的局限性。Jirka[17]建立了浮力射流在恒定流作用下的积分模型，该模型介绍了射流两种不同的剪切机制，还考虑了射流与环境流体之间的动压力，且将其近似转化为环境流体对射流的拖曳力作用。周连伟[18]采用动量积分法对非恒定环境中三维圆管浮射流进行研究，通过将非恒定问题转化成恒定问题的线性叠加，较准确地模拟预测了浮射流的运动轨迹以及稀释度变化等规律。Lin等[19]开发了一种新的积分模型来研究波浪对淹没浮力射流的影响，将波浪的作用作为外力纳入运动方程中，以模拟任意横截面上浮力射流的轨迹、速度分布和边界厚度。胡飞等[20]引入了射流流场保持瞬时稳定且相对速度剖面保持高斯分布的假设，对波浪作用影响的射流卷吸函数进行了修正，建立了波浪环境下垂直射流动量积分模型。Lai等[21]基于质量守恒（卷吸假定）、动量和浮力通量以及射流平均动量的衰减函数提出了浮射流的通用积分模型，并将射流掺混特性的模拟结果与实验观测结果进行了比较，发现两者基本吻合。Shrivastava等[22]提出了一种模拟浅水横流作用下多孔射流流场的积分模型，模拟结果与实测结果吻合良好，表明了所建立的数值模型较现有模型有明显改进。
如果射流所处海域的海水密度沿水深呈现不均匀分布时，射流与环境水体的密度差及其有效浮力的变化会对运动过程产生较大影响，针对此类现象，He和Lou[23]建立了积分模型来模拟线性分层环境中绕圆排列的多个强迫羽流的混合过程，基于该模型对线性分层环境中水平浮力射流进行了实验和数值模拟研究，结果表明水平浮力射流的动力学过程比垂直强迫羽流更为复杂，速度场和温度场均表现为水平区、上升区和振荡区，与稳定的密度分布相比，密度分层分布更有利于浮力射流的混合稀释[24–25]。
目前射流动量积分模型大多针对单一的波浪或水流或密度分层作用的情形来开发的，然而在污水排放的近岸海域环境中波浪和水流往往共生并存、相互影响。相较于前人[16, 19–20]建立的波浪环境下射流积分模型，本文将考虑环境水体中波浪与水流的共同作用，在控制方程中引入射流和波流之间的动压力，在此基础上构建一个波流共同作用环境下的射流积分模型，并基于该模型来模拟研究波流共同作用下动量射流的运动与稀释特性。考虑到污水排放射流近区段所处的海域水深相对较浅，环境水体的密度垂向分层效应往往并不明显，因此本文暂不考虑环境水体密度分层的影响。
2. 研究方法
2.1 积分模型
2.1.1 积分模型坐标系
图1为波流环境下任意角度排放射流的示意图，其中在全局笛卡尔坐标系，x表示波浪以及横流的传播方向；z表示逆重力向上的方向；uc表示射流中心轴速度；ua表示横流速度；δ表示射流中心轴线与x轴之间的角度；b表示射流半宽；直径为D的圆管射流位于（0，0，h0）处，其中h0是射流距离底部的高度；u0为射流的初始速度；ρ0为射流的初始密度；c0为射流的初始浓度。在局部圆柱坐标系中，沿射流轨迹定义，s为离射流口的轴向距离，r为距射流中心的径向距离，
$\phi $ 为射流截面上的方位角。射流单元体断面具有相应的单位流量通量Q、单位轴向动量通量M、单位浮力通量J和单位物质通量Qc。
图 1 使用全局坐标系和局部坐标系的射流排放到波流环境中的示意图（修改自方树桥[26]）Figure 1. Schematic diagram of a jet discharge into a wave current environment with global and local coordinate systems2.1.2 积分模型基本假设
（1） 瞬时稳定假设：参照Chin[16]提出的瞬时稳定假设，即射流在每一时刻相对于波浪运动均可以看成是一个稳定的状态。波流环境下射流呈现瞬时稳定态。
（2）环境流体假设：污水排放射流近区海域水深相对较浅，密度分层作用相对比较小，因此假设环境流体为密度均匀的不可压缩性流体；波浪为微幅波，基于线性波理论得到的由波浪引起的环境水体的速度分量为
$$ {\widetilde u = \frac{{ {\text{π}} H}}{T}\frac{{{\text{cosh}}\left( {kz} \right)}}{{{\text{sinh}}\left( {kh} \right)}}{\text{sin}}\left( {kx - \frac{{2 {\text{π}} }}{T}t} \right)} \text{，} $$ (1) $$ \widetilde w = \frac{{ {\text{π}} H}}{T}\frac{{{\text{sinh}}\left( {kz} \right)}}{{{\text{sinh}}\left( {kh} \right)}}{\text{cos}}\left( {kx - \frac{{2 {\text{π}} }}{T}t} \right)\text{，} $$ (2) 式中，
$ \widetilde u $ 和$ \widetilde w $ 分别为波浪水平与垂直速度分量；H为波高；k为波数（k = 2π/L），L为波长；T为周期；h为水深；x与z分别为水平与垂直坐标；t为时间。（3）初始排放条件假设：射流排放口为圆形，排放射流水体为不可压缩流体，其排放流量不随时间改变，排放口横断面上的密度、速度与浓度为均匀分布。
（4）布氏（Boussinesq）假设：射流与环境流体之间的密度差在惯性项中可以忽略，而在浮力项中则需要保留，且转换成为射流出口处密度的表达式。在此假设下进行断面积分时，密度差项可以射流出口处的密度作为参考密度，而将此参考密度提出积分号外简化积分方程式。
（5）射流流体假设：由射流运动自身引起，在射流圆形横断面上的轴向速度、密度差以及浓度分布具有自相似性，满足高斯分布；分子扩散效应较紊动扩散效应可忽略不计；流体的黏滞效应可以忽略。
根据Xu等[13]关于波流环境下射流三维结构的研究，射流在波流环境中存在类似于Jirka[17]的反向漩涡对结构，使波流环境下射流与环境水体界面上存在卷吸的流向与方位两种剪切机制。考虑到射流近区段的空间尺度相对较小，假设射流任意横断面上波浪水平与垂直速度分布的断面积分的平均值近似等于波浪水平与垂直速度分量在射流中心轴处的值，据此可认为整个射流横断面上环境水体的速度分量是均匀分布，由此得到耦合的环境水体速度
$ {u_s} = \sqrt {{{\left( {{u_a} + \widetilde u} \right)}^2} + {{\widetilde w}^2}} $ ，θ表示环境水体水平与垂直速度之间的夹角，如图1所示。基于以上假设，射流的速度、密度差与浓度函数可采用如下高斯分布函数：
$$ u = {u_c}{{\mathrm{e}}^{ - {r^2}/{b^2}}} + {u_s}{\text{cos}}\left( {\delta - \theta } \right)\text{，} $$ (3) $$ g' = {g'_c}{{\mathrm{e}}^{{{ - {r^2}} \mathord{/ {\vphantom {{ - {r^2}} {{{\left( {\lambda b} \right)}^2}}}} } {{{\left( {\lambda b} \right)}^2}}}}} \text{，} $$ (4) $$ c = {c_c}{{\mathrm{e}}^{{{ - {r^2}} \mathord{/ {\vphantom {{ - {r^2}} {{{\left( {\lambda b} \right)}^2}}}} } {{{\left( {\lambda b} \right)}^2}}}}} \text{，} $$ (5) 式中，
$ {u}_{c} $ 是射流的轴向速度；$g_c^{{'}}$ 是射流中心轴浮力加速度；${c_c}$ 是射流中心轴污染物浓度；$b$ 是射流半宽；$\lambda $ 表示流速剖面与密度差剖面宽度的比值。根据速度、密度差与浓度的分布特征，在横断面上进行积分，可以分别得到关于Q、M、J、Qc的表达式。
$$ Q = 2 {\text{π}} \mathop \int \nolimits_0^{{R_j}} ur{\mathrm{d}}r = {\text{π}} {b^2}\left[ {{u_c} + 2{u_s}{\text{cos}}\left( {\delta - \theta } \right)} \right]\text{，} $$ (6) $$ M = 2 {\text{π}} \mathop \int \nolimits_0^{{R_j}} {u^2}r{\mathrm{d}}r = \frac{1}{2} {\text{π}} {b^2}{\left[ {{u_c} + 2{u_s}{\text{cos}}\left( {\delta - \theta } \right)} \right]^2}\text{，} $$ (7) $$ J = 2 {\text{π}} \mathop \int \nolimits_0^{{R_j}} ug'r{\mathrm{d}}r = {\text{π}} {b^2}\left[ {{u_c}\frac{{{\lambda ^2}}}{{1 + {\lambda ^2}}} + {\lambda ^2}{u_s}{\text{cos}}\left( {\delta - \theta } \right)} \right]g_c^{{'}}\text{，} $$ (8) $$ {Q_c} = 2 {\text{π}} \mathop \int \nolimits_0^{{R_j}} ucr{\mathrm{d}}r = {\text{π}} {b^2}\left[ {{u_c}\frac{{{\lambda ^2}}}{{1 + {\lambda ^2}}} + {\lambda ^2}{u_s}{\text{cos}}\left( {\delta - \theta } \right)} \right]{c_c}. $$ (9) 2.1.3 控制方程的简化及推导
波流共同作用下射流在环境水体中的运动和稀释过程遵循流体力学基本运动定律，其运动控制方程的矢量形式可表达如下：
$$ \frac{{\partial \rho }}{{\partial t}} + \nabla \cdot \left( {\rho{\boldsymbol{ V}}} \right) = 0\text{，} $$ (10) $$ \rho \left( {\frac{{\partial \boldsymbol V}}{{\partial t}} + \left( { {\boldsymbol{V}} \cdot \nabla } \right) {\boldsymbol{V}}} \right) = - \nabla p + \rho {\boldsymbol{g}} + v{\nabla ^2} {\boldsymbol{V}}\text{，} $$ (11) $$ \frac{{\partial \varPhi }}{{\partial t}} + {{\boldsymbol{V}}} \cdot \left( {\nabla \varPhi } \right) = \nabla \cdot \left( {D\nabla \varPhi } \right)\text{，} $$ (12) 式中，ρ为密度；
$\boldsymbol {V} $ 为速度矢量；p为压力；$v$ 为黏性系数；Ф为标量；D为扩散系数；t为时间。为方便推导运动控制方程，选取三维空间中局部圆柱坐标系，根据基本假设对控制方程进行简化，并且对物理量做雷诺分解，分解为时均值和脉动值，可以得到如下控制方程：
连续方程为
$$ \frac{{\partial r\bar u}}{{\partial s}} + \frac{{\partial r\bar v}}{{\partial r}} = 0\text{，} $$ (13) 水平向动量方程为
$$\begin{split} &\left( {\bar u\frac{{\partial \bar u}}{{\partial s}} + \overline v \frac{{\partial \bar u}}{{\partial r}}} \right)\cos \delta - {\overline u ^2}\frac{{{\mathrm{d}}\delta }}{{{\mathrm{d}}s}}\sin \delta = \frac{1}{{{\rho _0}}}{\left( {\nabla \overline {p'} } \right)_x} +\\ &\qquad \frac{1}{r}\frac{{\partial r\overline {{{v'}^2}} }}{{\partial r}}\sin \delta - \frac{1}{r}\frac{{\partial r\overline {u'v'} }}{{\partial r}}\cos \delta \text{，} \end{split}$$ (14) 垂直向动量方程为
$$ \begin{split} &\left( {\bar u\frac{{\partial \bar u}}{{\partial s}} + \overline v \frac{{\partial \bar u}}{{\partial r}}} \right)\sin \delta + {\overline u ^2}\frac{{{\mathrm{d}}\delta }}{{{\mathrm{d}}s}}\cos \delta = \frac{{\overline {\Delta \rho } }}{{{\rho _0}}}g +\\ &\qquad\frac{1}{{{\rho _0}}}{\left( {\nabla \overline {p'} } \right)_z} - \frac{1}{r}\frac{{\partial r\overline {{{v'}^2}} }}{{\partial r}}\cos \delta - \frac{1}{r}\frac{{\partial r\overline {u'v'} }}{{\partial r}}\sin \delta \text{，}\end{split} $$ (15) 密度差方程为
$$ \bar u\frac{{\partial \overline {\Delta \rho } }}{{\partial s}} + \overline v \frac{{\partial \overline {\Delta \rho } }}{{\partial r}} = - \frac{1}{r}\frac{{\partial r\overline {v'\Delta \rho '} }}{{\partial r}} \text{，} $$ (16) 浓度扩散方程为
$$ \bar u\frac{{\partial \overline c }}{{\partial s}} + \overline v \frac{{\partial \overline c }}{{\partial r}} = - \frac{1}{r}\frac{{\partial r\overline {v'c'} }}{{\partial r}} \text{，} $$ (17) 式中，横线表示时间平均；上标符号（'）表示速度或浓度的脉动；
${\left( {\nabla \overline {p'} } \right)_x}$ 与${\left( {\nabla \overline {p'} } \right)_z}$ 是$\nabla \overline {p'} $ 在x与z方向上的分量，其中$p'$ 是环境水体的静水压力pa与射流内部的压力p之差。为求解上述控制方程，需要一定的边界条件来闭合方程。在射流逐渐发展完全后，当沿着射流径向方向往远处推移时，射流边界的射流流体速度将趋于环境流体的速度，这时射流边界可视为一稳定的边界条件，可用下式表示
$$ \left\{ \begin{gathered} \bar u = {u_s} , \\ \bar v = - {E \mathord{\left/ {\vphantom {E {\left( {2{\text{π}} r} \right)}}} \right. } {\left( {2{\text{π}} r} \right)}} , \\ \end{gathered} \right.{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} r \to \infty \text{，} $$ (18) 式中，
$\infty $ 表示环境流场；E表示卷吸函数，满足关系式如下：$$ E = \frac{\partial }{{\partial s}}\int_0^\infty {2{\text{π}} \bar ur{\mathrm{d}}r} . $$ (19) 在给定边界条件的基础上，对上述控制方程两边同乘
$ \text{2{\text{π}}r} $ ，从边界r = 0积分到r =$\infty $ ，代入边界条件，并运用分部积分法进行化简，可以得到积分形态的控制方程组。连续方程为
$$ \frac{{{\mathrm{d}}Q}}{{{\mathrm{d}}s}} = \frac{{\mathrm{d}}}{{{\mathrm{d}}s}}\int_0^\infty {2{\text{π}} \bar ur{\mathrm{d}}r} = - 2{\text{π}} \mathop {\lim }\limits_{r \to \infty } \left( {r\bar v} \right) = E\text{，} $$ (20) 水平向动量方程为
$$ \frac{{{\mathrm{d}}M\cos \delta }}{{{\mathrm{d}}s}} = E{u_s}\cos \theta + \frac{{\cos \theta - \cos \delta \cos \left( {\delta - \theta } \right)}}{{\left| {\cos \theta - \cos \delta \cos \left( {\delta - \theta } \right)} \right|}}{F_D}\sin \delta \text{，} $$ (21) 垂直向动量方程为
$$ \begin{split}\frac{{{\mathrm{d}}M\sin \delta }}{{{\mathrm{d}}s}} =\ & E{u_s}\sin \theta + {\text{π}} {\lambda ^2}{b^2}{g'_c} -\\ & \frac{{\cos \theta - \cos \delta \cos \left( {\delta - \theta } \right)}}{{\left| {\cos \theta - \cos \delta \cos \left( {\delta - \theta } \right)} \right|}}{F_D}\cos \delta \text{，} \end{split}$$ (22) 密度差方程为
$$ \frac{{{\mathrm{d}}J}}{{{\mathrm{d}}s}} = \frac{g}{{{\rho _0}}} \cdot 2{\text{π}} \mathop \int \nolimits_0^\infty \frac{{\partial \overline {u\Delta \rho r} }}{{\partial s}}{\mathrm{d}}r = 0\text{，} $$ (23) 浓度扩散方程为
$$ \frac{{{\mathrm{d}}{Q_c}}}{{{\mathrm{d}}s}} = 2{\text{π}} \mathop \int \nolimits_0^\infty \frac{{\partial \overline {ucr} }}{{\partial s}}{\mathrm{d}}r = 0\text{，} $$ (24) 根据射流运动轨迹的几何特性，可以得到以下两个方程为
$$ \frac{{{\mathrm{d}}x}}{{{\mathrm{d}}s}} = {\text{cos}}\;\delta \text{，} $$ (25) $$ \frac{{{\mathrm{d}}z}}{{{\mathrm{d}}s}} = {\text{sin}}\;\delta \text{.} $$ (26) 式（20）至式（26）构成了波流环境下射流动量积分模型的常微分方程组，可利用一维差分格式，使用四阶龙格库塔算法对常微分方程组进行数值求解[26]。
在求解动量方程（21）和（22）过程中，E和FD分别表示卷吸周围环境水体的水通量和作用于射流体上的环境拖曳力，E和FD构成了积分公式中的“紊动闭合条件”。在波流共同作用下，射流的卷吸主要由紊动卷吸、浮力卷吸、波流产生的附加卷吸以及射流与波流之间的方位剪切产生卷吸这4个部分组成。参照Jirka[17]的处理方式，可以用下式来表达E：
$$ \begin{split} E=&2\mathrm{\text{π}}bu_c\left[\alpha_1+\alpha_2\frac{\text{sin}\; \delta}{F_l^2}+\alpha_3\frac{u_s\text{cos}\left(\delta-\theta\right)}{u_c+u_s}\right]+ \\ & 2\alpha_4\text{π}bu_s\sqrt{1-\text{co}\text{s}^2\left(\delta-\theta\right)}\left|\text{cos}\left(\delta-\theta\right)\right|\text{，} \end{split} $$ (27) 式中，α1、α2、α3和α4为卷吸系数。本文参照方树桥[26]的研究成果，将上述卷吸系数取值为
$$ {\alpha _1} = 0.055,{\text{ }}{\alpha _2} = 0.6,{\text{ }}{\alpha _3} = 0.055,{\text{ }}{\alpha _4} = 0.5. $$ (28) 在波流共同作用下射流与周围流体之间动压力较大，需要考虑动压力分布不均匀对射流运动的影响。参照Jirka[17]的处理方式，将这种影响近似为环境水体对射流的拖曳力FD，其相应的表达式为
$$ {F_D} = 2{\text{π}} \int_0^\infty {\frac{{\nabla \overline {p'} }}{{{\rho _0}}}r{\mathrm{d}}r} = \sqrt 2 {c_D}bu_s^2\left[ {1 - {\text{co}}{{\text{s}}^2}\left( {\delta - \theta } \right)} \right]\text{，} $$ (29) 式中，
$ {u_s}\sqrt {1 - {{\cos }^2}\left( {\delta - \theta } \right)} $ 是射流断面环境水体横向速度分量；$ \sqrt 2 b $ 是射流展宽；cD是拖曳力系数。方树桥[26]通过与多组次实验结果的对比分析研究，发现cD和射流波浪特征速度比Rw = u0/uw具有很好的相关关系，可用以下函数方程式来表达$$ {c_D} = \frac{{1.3R_w^2 - 65.07{R_w} + 1\;636}}{{R_w^2 - 64.52{R_w} + 1\;410}} . $$ (30) 2.2 射流特征参数的定义
根据Xu等[15]对于波流环境下射流的研究成果，射流在波流环境中受到横流的作用而发生方向的偏转，并在波浪的作用下发生周期性的摆动，射流的运动扩散和初始稀释受到两者的共同作用。考虑到波浪的周期性变化，波浪周期内垂直射流孔处波浪诱导水平速度的平均值用uw0表示，用于表征一个波周期内波浪作用的整体效应。根据线性波理论，uw0的表达式如下所示：
$$ {u_{w0}} = \frac{1}{T}\mathop \int \nolimits_0^T {u_w}\left| {{\text{cos}}\;\omega t} \right|{\mathrm{d}}t = {\alpha _{wc}}{u_w}\text{，} $$ (31) 式中，αwc表示波流相互作用系数，可取值为0.637[15]；uw表示波浪特征速度，定义为射流出口处最大水平波浪速度，根据线性波理论，uw可用以下公式计算：
$$ {u_w} = \frac{{{\text{π}} H}}{T}\frac{{\cosh (k{h_0})}}{{\sinh (kh)}}\text{，} $$ (32) 环境水体的特征速度为波浪特征速度与横流的线性叠加，表达式为
$$ {u_{ch}} = {u_a} + {u_{w0}} = {u_a} + {\alpha _{wc}}{u_w}\text{，} $$ (33) 对于非浮力射流，其特征长度l可定义为
$$ l = \frac{{M_0^{1/2}}}{{{u_{ch}}}}\text{，} $$ (34) 式中，M0表示射流初始动量，表达式为
$$ {M_0} = \frac{1}{4}{\text{π}} {D^2}u_0^2\text{，} $$ (35) 对于浮力射流，其特征长度可定义为
$$ {l_{mb}} = {{M_0^{{1/ 4}}J_0^{{1 / 2}}}/ {u_{ch}^2}} \text{，} $$ (36) 式中，J0表示为射流初始浮力通量，表达式为
$$ {\kern 1pt} {J_0} = {{\frac{1}{4}{\text{π}} {D^2}{u_0}\left( {{\rho _a} - {\rho _0}} \right)g} / {{\rho _0}}} \text{，} $$ (37) 为了表征射流沿程稀释的快慢，可以引入最小稀释度这一特征参数，其定义式为
$$ {S_c} = {c_0}/{C_m}\text{，} $$ (38) 式中，Cm为射流沿程横截面浓度的最大值，其所处的垂向距离为Zm。
2.3 量纲分析
根据Xu等[15]的量纲分析结果，波流环境下无浮力射流横断面最小稀释度的垂向位置Zm和最小稀释度Sc函数关系式可以分别表示为
$$ \frac{{{Z_m}}}{l} = {f_1}\left(\frac{x}{l}\right) \text{，} $$ (39) $$ {S_c} = {f_2}\left(\frac{x}{l},\frac{{{u_{ch}}}}{{{u_a}}},R,{S_t}\right) \text{，} $$ (40) 式中，uch/ua为波流特征速度与横流速度比；R为射流与横流速度比；Rwa为波浪与横流速度比；St为Strouhal数。
$$ \frac{u_{ch}}{u_a}=1+\alpha_{wc}R_{wa}\text{，} $$ (41) $$ R = \frac{{{u_0}}}{{{u_a}}}\text{，} $$ (42) $$ R_{wa}= \frac{{u_w}}{{{u_a}}} \text{，} $$ (43) $$ S_t=\frac{D}{u_aT}. $$ (44) 3. 结果与分析
3.1 模型验证分析
3.1.1 波流环境下非浮力射流
王娅娜[12]开展了波流环境下非浮力射流的物理实验，其实验条件如表1所示。在所有试验组中，静水深为0.5 m，射流圆管直径为0.01 m，射流口离波流水槽底部上方0.1 m处。
表 1 波流环境下非浮力射流实验组次条件Table 1. Experimental conditions of non-buoyant jets in wavy crossflow environments组次 射流初速度
u0/(m·s−1)横流速度
ua/(m·s−1)波浪周期
T/s波浪波高
H/cmRw A1 0.499 0.038 6 1.0 3.0 19.1 A2 0.499 0.038 6 1.4 3.0 11.2 B1 0.760 0.038 6 1.0 3.0 29.1 B2 0.760 0.038 6 1.4 3.0 17.0 C1 1.017 0.038 6 1.0 3.0 39.0 C2 1.017 0.038 6 1.4 3.0 22.7 D1 0.499 0.077 6 1.0 3.0 19.1 D2 0.499 0.077 6 1.4 3.0 11.2 E1 0.760 0.077 6 1.0 3.0 29.1 E2 0.760 0.077 6 1.4 3.0 17.0 F1 1.017 0.077 6 1.0 3.0 39.0 F2 1.017 0.077 6 1.4 3.0 22.7 根据式（30）计算得到各组次的cD值，将其代入模型中计算不同波流环境下非浮力射流的稀释过程，并与实验结果[12]进行比较。图2给出了A1～F1组次射流横截面最小稀释度垂向位置Zm和最小稀释度Sc的对比结果，从图中可以看出数模结果与物理实验结果吻合良好，说明动量积分模型可以较好地模拟非浮力射流沿程的时均运动与稀释过程。
图 2 波流环境下射流最小稀释度垂向位置和最小稀释度物理与数值结果对比Figure 2. Comparison of physical and numerical results of the vertical position of minimum dilution and the minimum dilution of jets in wavy crossflow environments3.1.2 波流环境下浮力射流
Xu等[27]对波流环境下浮力射流进行了物理实验研究，具体的实验条件如表2所示。试验组次的静水深均为0.6 m，射流圆管直径均为0.01 m，射流口在离波流水槽底部上方0.1 m处。类似地，模型中cD的取值由式（30）计算得到。
表 2 波流环境下浮力射流实验组次条件Table 2. Experimental conditions of buoyant jets in wavy crossflow environments组次 射流初速度
u0/(m·s−1)横流速度
ua/(m·s−1)波浪周期
T/s波浪波高
H/cm无量纲密度差
Δρ/ρ0Rw JB1 0.180 0.025 1 1.0 3.0 0.7% 6.89 JB2 0.180 0.026 4 1.0 3.0 1.3% 6.89 JB3 0.180 0.038 0 1.0 3.0 0.7% 6.89 JB4 0.180 0.041 7 1.0 3.0 1.3% 6.89 图3为JB1～JB4组次浮射流横截面最小稀释度垂向位置Zm和最小稀释度Sc与实验数据的对比。数值计算结果与实验结果吻合较好，说明上述卷吸系数和cD的取值在本文模型中也是合理的。
图 3 波流环境下浮射流最小稀释度垂向位置和最小稀释度物理与数值结果对比Figure 3. Comparison of physical and numerical results of the vertical position of minimum dilution and the minimum dilution of buoyant jets in wavy crossflow environments3.1.3 波流环境下射流浓度云图
以D1工况为例，采用本模型计算模拟了波流环境下射流在4个不同的相位时刻的浓度云图，如图4所示。从图中可以看到，射流受到波浪与横流的共同作用。在横流作用下，射流在出口附近发生弯曲，向横流方向偏转，并且在波浪的作用下，发生上下摆动。
图 4 波流环境下射流在一个波周期内的浓度云图（以 D1 为例）Figure 4. Concentration distributions within one wave period of a jet (taking D1 for example) in a wavy crossflow environment为了对比分析波浪对射流扩散与稀释的影响，继续以D1数值工况为例，绘制波流与横流环境下射流的平均浓度等值线图，如图5所示（D0即仅横流作用）。可以发现波浪的振荡作用使得射流的轨迹线更加弯曲，射流的影响范围更宽，相同高度下射流的稀释程度更高，因此波浪的存在有助于加快射流在近区段的稀释过程。
图 5 波流与横流环境下射流平均浓度等值线的对比（以D1为例）Figure 5. Comparison of contour lines of average concentration for a jet (taking D1 for example) in wavy crossflow and crossflow only environments3.2 卷吸系数敏感性分析
通过对波流环境下射流的卷吸系数α1、α2、α3和α4的敏感性分析，以定量分析比较波流环境下射流过程中不同卷吸的贡献。
3.2.1 紊动卷吸系数敏感性分析(α1)
α1表示紊动卷吸系数，它是一个常量且等于静水环境中射流的卷吸系数，通常取值为0.055，本文不作特别讨论。
3.2.2 纯羽流卷吸系数的敏感性分析(α2)
在波流环境下，对不同α2值（0.3、0.6、0.8）下浮力射流（以JB1为例）的最小稀释度Sc和垂向位置Zm与实验数据进行了比较，如图6所示。垂向位置Zm的模拟结果对α2的取值不敏感，而最小稀释度Sc的模拟结果对α2的取值敏感，且随α2的增大而增大。这一现象是可预期的，因为随着α2的增大，射流中环境水的卷吸量增加。当α2 = 0.6时，最小稀释度的模拟结果与实验数据吻合最好。
图 6 波流环境下浮射流在不同α2值（0.3、0.6、0.8）下的最小稀释度和垂向位置的模型预测与实验数据的比较Figure 6. Comparison of minimum dilution and vertical location of model prediction with experimental data for different values of α2 (0.3, 0.6, 0.8) for buoyant jets in wavy crossflow environments3.2.3 纯尾流卷吸系数的敏感性分析(α3)
在波流环境下，对不同α3值（0.025、0.055、0.075）下射流（以D1为例）的最小稀释度Sc和垂向位置Zm与实验数据进行了比较，以0.055值相对更优，如图7所示。最小稀释度Sc与垂向位置Zm的模拟结果对α3的取值不太敏感，这可能与射流运动过程中纯尾流存在较少有关。
图 7 波流环境下射流在不同α3值（0.025、0.055、0.075）下的最小稀释度和垂向位置的模型预测与实验数据的比较Figure 7. Comparison of minimum dilution and vertical location of model prediction with experimental data for different values of α3 (0.025, 0.055, 0.075) for jets in wavy crossflow environments3.2.4 方位剪切卷吸系数的敏感性分析(α4)
在波流环境下，对不同α4值（0.2、0.5、0.7）下射流（以D1为例）的最小稀释度Sc和垂向位置Zm与实验数据进行了比较，如图8所示。最小稀释度Sc的模拟结果随着α4的增大而增大，且射流偏转略有减小。这一现象也是可预期的，因为随着α4的增大，射流中环境水的卷吸量增加。当α4 = 0.5时，最小稀释度的模拟结果与实验数据吻合最好。
图 8 波流环境下射流在不同α4值（0.2、0.5、0.7）下最小稀释度和垂向位置的模型预测与实验数据的比较Figure 8. Comparison of minimum dilution and vertical location of model prediction with experimental data for different values of α4 (0.2, 0.5, 0.7) for jets in wavy crossflow environments3.3 波流环境下射流在近区段的稀释特性研究
基于已验证的波流环境下射流动量积分模型，可以开展更多组次的数值实验计算，通过波浪、水流与射流参数的组合（表3），对比分析不同波流环境下射流在近区段的运动与稀释规律，在此基础上，根据斯特劳哈尔数St、射流–横流速度比R、波浪–横流速度比Rwa等无量纲特征参数[15]，以综合分析不同环境因子对射流沿程稀释的影响程度；采用量纲分析与数据拟合相结合方法，构建射流轨迹中心位置及最小稀释度等特征参数与环境动力因子之间的无量纲经验关系，为后续开展波流环境下射流近、远区耦合计算提供快速、可靠的射流初始稀释条件。受篇幅限制，本文暂不考虑射流的初始浮力效应，所得到经验公式仅适用于射流水体与周边水体不存在密度差的情形，关于波流环境下浮力射流在近区段的稀释特性研究成果将另文发表。
表 3 波流环境下射流数值实验组次Table 3. Numerical experiments of jets in wavy crossflow environments数值
组次射流速度
u0/(m·s−1)横流速度
ua/(m·s−1)波周
期T/s波高
H/cm射流横流
速度比R波浪横流
速度比Rwa斯特劳哈
尔数StJ1 0.72 0.06 1.0 1.035 12 0.15 0.17 J2 0.72 0.06 1.5 0.568 12 0.15 0.11 J3 0.72 0.06 2.0 0.486 12 0.15 0.083 J4 0.72 0.06 1.0 2.415 12 0.35 0.17 J5 0.72 0.06 1.5 1.326 12 0.35 0.11 J6 0.72 0.06 2.0 1.128 12 0.35 0.083 J7 0.72 0.06 1.0 3.795 12 0.55 0.17 J8 0.72 0.06 1.5 2.083 12 0.55 0.11 J9 0.72 0.06 2.0 1.773 12 0.55 0.083 J10 0.60 0.06 1.0 1.035 10 0.15 0.17 J11 0.60 0.06 1.5 0.568 10 0.15 0.11 J12 0.60 0.06 2.0 0.486 10 0.15 0.083 J13 0.60 0.06 1.0 2.415 10 0.35 0.17 J14 0.60 0.06 1.5 1.326 10 0.35 0.11 J15 0.60 0.06 2.0 1.128 10 0.35 0.083 J16 0.60 0.06 1.0 3.795 10 0.55 0.17 J17 0.60 0.06 1.5 2.083 10 0.55 0.11 J18 0.60 0.06 2.0 1.773 10 0.55 0.083 J19 0.48 0.06 1.0 1.035 8 0.15 0.17 J20 0.48 0.06 1.5 0.568 8 0.15 0.11 J21 0.48 0.06 2.0 0.486 8 0.15 0.083 J22 0.48 0.06 1.0 2.415 8 0.35 0.17 J23 0.48 0.06 1.5 1.326 8 0.35 0.11 J24 0.48 0.06 2.0 1.128 8 0.35 0.083 J25 0.48 0.06 1.0 3.795 8 0.55 0.17 J26 0.48 0.06 1.5 2.083 8 0.55 0.11 J27 0.48 0.06 2.0 1.773 8 0.55 0.083 3.3.1 波流环境下射流轨迹中心线位置
为了更为直观表述射流的运动形态，可以将射流横截面最小稀释度所在位置Zm定义为射流轨迹中心位置。图9状态A显示了斯特劳哈尔数St、射流–横流速度比R、波浪–横流速度比Rwa等参数对轨迹中心线位置沿下游距离变化规律的影响。从图9a中可以看出，斯特劳哈尔数St对射流轨迹中心线位置的影响很小，基本可以忽略不计；从图9b中可以看出，随着射流–横流速度比R的增加，射流轨迹中心线位置有较为明显的抬高趋势；从图9c中可以看出，随着波浪–横流速度比Rwa的增加，射流轨迹中心线位置有较为明显的下降趋势，这些定性的规律与实验观测结果是完全一致的[12]。
图 9 波流环境下射流轨迹中心线位置沿下游距离的变化关系Figure 9. The variation relationship of the centerline position of jet trajectory along the downstream distance for jets in wavy crossflow environments为了建立射流轨迹中心线位置Zm与环境动力要素之间的量化关系，首先对图9状态A中横、纵坐标轴上的变量都乘以D/l，其中l由式（34）所定义，它反映了射流初始速度与波流速度之间的相对大小；然后将Zm/l与沿下游距离x/l建立关系，如图9状态B所示。从图9d至图9f中可以看出，每个数值实验工况下，Zm/l沿x/l的抬升速率是近似相同的，因此对于Zm可以采用以下一般形式来描述：
$$ \frac{{{Z_m}}}{l} = {{{C}}_1}{\left( {\frac{x}{l}} \right)^{{{{C}}_2}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \text{，} $$ (45) 式中，C1、C2为拟合系数，可以通过对动量积分模拟结果的最小二乘曲线拟合来确定。图9g展示了Zm沿程变化的拟合曲线及相应的无量纲经验公式：
$$ \frac{{{Z_m}}}{l} = {\text{1}}{\text{.934}}{\left( {\frac{x}{l}} \right)^{{\text{0}}{\text{.32}}}}{\kern 1pt} {\kern 1pt} {\kern 1pt}\qquad 0.2<x/l<6 . $$ (46) 3.3.2 波流环境下射流最小稀释度沿程分布
在对排海工程的环境影响分析中，除了掌握射流轨迹中心线位置沿程的变化规律外，还需要了解其所在位置的最小稀释度，它在一定程度上反映了射流在初始稀释过程中所能达到的最大稀释能力。
图10状态A为上述3个无量纲特征参数对最小稀释度Sc沿下游距离x/D变化规律的影响。从图10a可以看出，最小稀释度Sc随着St（R和Rwa的值控制不变）的增加而略有减小；从图10b和图10c可以看出，Sc随着R（St和Rwa的值控制不变）和Rwa（St和R的值控制不变）的增加而增加。类似地，对图10状态A中横、纵坐标轴上的变量都乘以无量纲组合特征参数D/l，然后分析最小稀释度ScD/l与下游距离x/l之间的关系，如图10状态B所示。由图可以看出，St和R对无量纲化断面最小稀释度ScD/l的作用较小（图10d和图10e），可以忽略不计；但Rwa的影响还是比较明显的（图10f），说明无量纲参数ScD/l还没有很好地反映波流环境动力变化的综合影响。
图 10 波流环境下射流最小稀释度与下游距离的变化关系Figure 10. The variation relationship of the minimum dilution along the downstream distance for jets in wavy crossflow environments为此，对图10状态B中每个纵坐标轴上变量都乘以无量纲组合特征参数
$ {{u_a^2}/{u_{ch}^2}} $ ，得到无量纲化的最小稀释度$ {{{S_c}Du_a^2} / {u_{ch}^2l}} $ ，并绘制其与下游距离x/l之间关系，如图10状态C所示。从图10g至图10j中可以看出，每个数值实验工况$ {{{S_c}Du_a^2}/ {u_{ch}^2l}} $ 随x/l的变化趋势近似相同的，因此可以建立波流环境下射流最小稀释度沿程变化的一般表达式：$$ \frac{{{S_c}Du_a^2}}{{u_{ch}^2l}} = {{{C}}_3}{\left( {\frac{x}{l}} \right)^{{C_4}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \text{，} $$ (47) 式中，C3、C4为拟合系数，可以通过对动量积分模拟结果的最小二乘曲线拟合来确定。图10j展示了射流断面最小稀释度沿程变化的拟合曲线及相应的无量纲经验公式：
$$ \frac{{{S_c}Du_a^2}}{{u_{ch}^2l}} = {\text{0}}{\text{.702\;4}}{\left( {\frac{x}{l}} \right)^{{\text{0}}{\text{.57}}}}{\kern 1pt} {\kern 1pt} {\kern 1pt}\qquad0.2<x/l<6 . $$ (48) 需要指出的是，本文所提出的公式是基于动量积分模型多组次数值实验结果得到的，它可以较好地反映波流共同作用下射流时均的运动状态和稀释程度。由于做了动量积分的处理，本文所采用的射流轨迹中心线位置和断面最小稀释度的定义与基于三维大涡模拟结果所给出的定义[15]是有所差异的。考虑到排海射流在远区的稀释与扩散过程多由潮流或沿岸流所控制，其数值模拟多采用基于雷诺时间平均的紊流模型来开展，因此在未来的射流近远区耦合计算中，可以采用上述经验公式来计算射流在近区段沿程的平均稀释度，并为远区模型提供必要的初始稀释条件。在本文所提出的公式中由于没有考虑浮力的影响，因此仅适用于排放水体与周边水体不存在密度差的情形。
4. 结论
本文在合理假设条件的基础上，对射流运动控制方程进行积分，建立了一种适用于波流环境下射流的动量积分模型；通过与实验数据对比验证，确定了相应的卷吸与拖曳力系数，验证了模型的合理性和通用性。基于动量积分模型模拟分析了波流环境下射流的运动和稀释特性，通过对比研究发现，相较于单一的横流作用，射流在波流共同作用下发生振荡，射流的范围较横流中更大一些，射流的稀释能力可以得到一定程度的增强。基于多组次的数值模拟结果，分析了斯特劳哈尔数St、射流–横流速度比R、波浪–横流速度比Rwa等无量纲特征参数对射流稀释度沿程变化的影响，通过无量纲分析与最小二乘拟合，建立了波流环境下射流轨迹线位置和最小稀释度沿程变化的经验公式。需要说明的是，该公式仅适用于排放水体与周边水体不存在密度差的情形，关于波流环境下浮力射流在近区段的运动和稀释特性研究成果将另文予以发表。
-
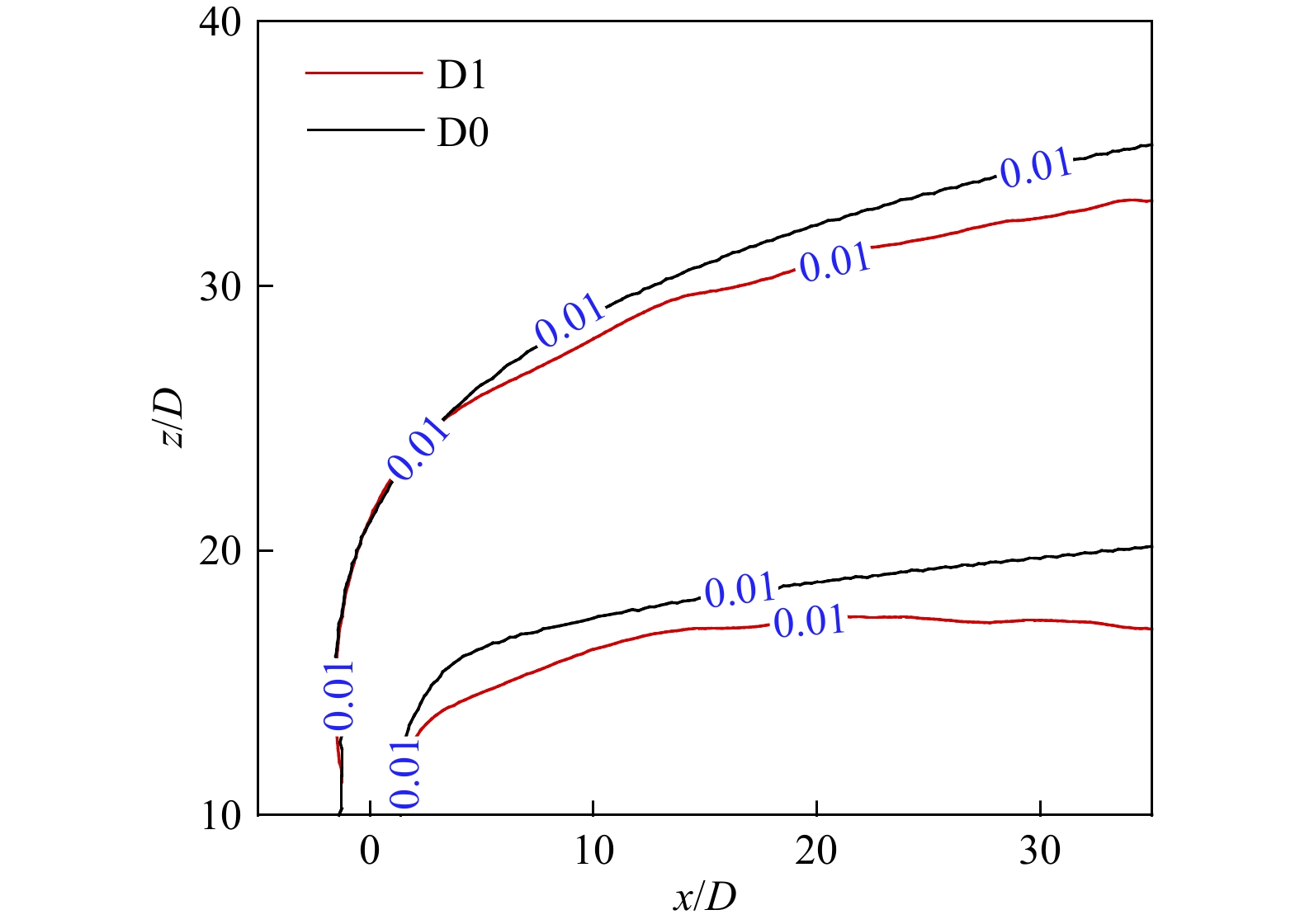
图 1 使用全局坐标系和局部坐标系的射流排放到波流环境中的示意图（修改自方树桥[26]）
Fig. 1 Schematic diagram of a jet discharge into a wave current environment with global and local coordinate systems
图 2 波流环境下射流最小稀释度垂向位置和最小稀释度物理与数值结果对比
Fig. 2 Comparison of physical and numerical results of the vertical position of minimum dilution and the minimum dilution of jets in wavy crossflow environments
图 3 波流环境下浮射流最小稀释度垂向位置和最小稀释度物理与数值结果对比
Fig. 3 Comparison of physical and numerical results of the vertical position of minimum dilution and the minimum dilution of buoyant jets in wavy crossflow environments
图 4 波流环境下射流在一个波周期内的浓度云图（以 D1 为例）
Fig. 4 Concentration distributions within one wave period of a jet (taking D1 for example) in a wavy crossflow environment
图 5 波流与横流环境下射流平均浓度等值线的对比（以D1为例）
Fig. 5 Comparison of contour lines of average concentration for a jet (taking D1 for example) in wavy crossflow and crossflow only environments
图 6 波流环境下浮射流在不同α2值（0.3、0.6、0.8）下的最小稀释度和垂向位置的模型预测与实验数据的比较
Fig. 6 Comparison of minimum dilution and vertical location of model prediction with experimental data for different values of α2 (0.3, 0.6, 0.8) for buoyant jets in wavy crossflow environments
图 7 波流环境下射流在不同α3值（0.025、0.055、0.075）下的最小稀释度和垂向位置的模型预测与实验数据的比较
Fig. 7 Comparison of minimum dilution and vertical location of model prediction with experimental data for different values of α3 (0.025, 0.055, 0.075) for jets in wavy crossflow environments
图 8 波流环境下射流在不同α4值（0.2、0.5、0.7）下最小稀释度和垂向位置的模型预测与实验数据的比较
Fig. 8 Comparison of minimum dilution and vertical location of model prediction with experimental data for different values of α4 (0.2, 0.5, 0.7) for jets in wavy crossflow environments
图 9 波流环境下射流轨迹中心线位置沿下游距离的变化关系
Fig. 9 The variation relationship of the centerline position of jet trajectory along the downstream distance for jets in wavy crossflow environments
图 10 波流环境下射流最小稀释度与下游距离的变化关系
Fig. 10 The variation relationship of the minimum dilution along the downstream distance for jets in wavy crossflow environments
表 1 波流环境下非浮力射流实验组次条件
Tab. 1 Experimental conditions of non-buoyant jets in wavy crossflow environments
组次 射流初速度
u0/(m·s−1)横流速度
ua/(m·s−1)波浪周期
T/s波浪波高
H/cmRw A1 0.499 0.038 6 1.0 3.0 19.1 A2 0.499 0.038 6 1.4 3.0 11.2 B1 0.760 0.038 6 1.0 3.0 29.1 B2 0.760 0.038 6 1.4 3.0 17.0 C1 1.017 0.038 6 1.0 3.0 39.0 C2 1.017 0.038 6 1.4 3.0 22.7 D1 0.499 0.077 6 1.0 3.0 19.1 D2 0.499 0.077 6 1.4 3.0 11.2 E1 0.760 0.077 6 1.0 3.0 29.1 E2 0.760 0.077 6 1.4 3.0 17.0 F1 1.017 0.077 6 1.0 3.0 39.0 F2 1.017 0.077 6 1.4 3.0 22.7 
下载: 导出CSV
表 2 波流环境下浮力射流实验组次条件
Tab. 2 Experimental conditions of buoyant jets in wavy crossflow environments
组次 射流初速度
u0/(m·s−1)横流速度
ua/(m·s−1)波浪周期
T/s波浪波高
H/cm无量纲密度差
Δρ/ρ0Rw JB1 0.180 0.025 1 1.0 3.0 0.7% 6.89 JB2 0.180 0.026 4 1.0 3.0 1.3% 6.89 JB3 0.180 0.038 0 1.0 3.0 0.7% 6.89 JB4 0.180 0.041 7 1.0 3.0 1.3% 6.89
下载: 导出CSV
表 3 波流环境下射流数值实验组次
Tab. 3 Numerical experiments of jets in wavy crossflow environments
数值
组次射流速度
u0/(m·s−1)横流速度
ua/(m·s−1)波周
期T/s波高
H/cm射流横流
速度比R波浪横流
速度比Rwa斯特劳哈
尔数StJ1 0.72 0.06 1.0 1.035 12 0.15 0.17 J2 0.72 0.06 1.5 0.568 12 0.15 0.11 J3 0.72 0.06 2.0 0.486 12 0.15 0.083 J4 0.72 0.06 1.0 2.415 12 0.35 0.17 J5 0.72 0.06 1.5 1.326 12 0.35 0.11 J6 0.72 0.06 2.0 1.128 12 0.35 0.083 J7 0.72 0.06 1.0 3.795 12 0.55 0.17 J8 0.72 0.06 1.5 2.083 12 0.55 0.11 J9 0.72 0.06 2.0 1.773 12 0.55 0.083 J10 0.60 0.06 1.0 1.035 10 0.15 0.17 J11 0.60 0.06 1.5 0.568 10 0.15 0.11 J12 0.60 0.06 2.0 0.486 10 0.15 0.083 J13 0.60 0.06 1.0 2.415 10 0.35 0.17 J14 0.60 0.06 1.5 1.326 10 0.35 0.11 J15 0.60 0.06 2.0 1.128 10 0.35 0.083 J16 0.60 0.06 1.0 3.795 10 0.55 0.17 J17 0.60 0.06 1.5 2.083 10 0.55 0.11 J18 0.60 0.06 2.0 1.773 10 0.55 0.083 J19 0.48 0.06 1.0 1.035 8 0.15 0.17 J20 0.48 0.06 1.5 0.568 8 0.15 0.11 J21 0.48 0.06 2.0 0.486 8 0.15 0.083 J22 0.48 0.06 1.0 2.415 8 0.35 0.17 J23 0.48 0.06 1.5 1.326 8 0.35 0.11 J24 0.48 0.06 2.0 1.128 8 0.35 0.083 J25 0.48 0.06 1.0 3.795 8 0.55 0.17 J26 0.48 0.06 1.5 2.083 8 0.55 0.11 J27 0.48 0.06 2.0 1.773 8 0.55 0.083
下载: 导出CSV
-
[1] 郭振仁. 污水排放工程水力学[M]. 北京: 科学出版社, 2001.Guo Zhenren. Hydraulics of Polluted Water Discharge Engineering[M]. Beijing: Science Press, 2001. [2] Choi K W, Lee J H. Distributed entrainment sink approach for modeling mixing and transport in the intermediate field[J]. Journal of Hydraulic Engineering, 2007, 133(7): 804−815. doi: 10.1061/(ASCE)0733-9429(2007)133:7(804) [3] 徐振山, 陈永平, 张长宽. 海岸动力环境下射流运动研究综述[J]. 水科学进展, 2012, 23(3): 438−444.Xu Zhenshan, Chen Yongping, Zhang Changkuan. Review of hydrodynamics of jet flow in coastal waters[J]. Advances in Water Science, 2012, 23(3): 438−444. [4] 姜国强, 李炜. 横流中有限宽窄缝射流的旋涡结构[J]. 水利学报, 2004, 35(5): 52−57, 63.Jiang Guoqiang, Li Wei. Vortex structure of slot turbulent jets in cross-flow[J]. Journal of Hydraulic Engineering, 2004, 35(5): 52−57, 63. [5] 姜国强, 李炜, 陶建华. 动水环境中有限宽窄缝湍射流的水力特性研究[J]. 水利学报, 2004, 35(12): 51−55, 61.Jiang Guoqiang, Li Wei, Tao Jianhua. Study on vertical turbulent slot jet impinging into cross flow[J]. Journal of Hydraulic Engineering, 2004, 35(12): 51−55, 61. [6] 周丰, 孙昭晨, 梁书秀. 波浪环境中圆形垂向射流的试验研究[J]. 水利学报, 2007, 38(8): 981−985, 990.Zhou Feng, Sun Zhaochen, Liang Shuxiu. Experimental study on vertical round jet discharged into wave environment with definite depth[J]. Journal of Hydraulic Engineering, 2007, 38(8): 981−985, 990. [7] Anghan C, Bade M H, Banerjee J. A review on fundamental properties of the jet in the wave environment[J]. Ocean Engineering, 2022, 250: 110914. doi: 10.1016/j.oceaneng.2022.110914 [8] Anghan C, Bade M H, Banerjee J. Direct numerical simulation of turbulent round jet released in regular waves[J]. Applied Ocean Research, 2022, 125: 103248. doi: 10.1016/j.apor.2022.103248 [9] Abdel-Rahman A A, Eleshaky M E. Diffusion characteristics of a plane jet discharged in a wavy crossflowing stream[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2004, 218(4): 411−423. [10] 袁丽蓉. 波流环境中垂向紊动射流的数值模拟研究[D]. 大连: 大连理工大学, 2006.Yuan Lirong. Numerical study on vertical turbulent jet in waves and currents[D]. Dalian: Dalian University of Technology, 2006. [11] 鲁俊, 王玲玲, 曹小红. 横流中射流及其温度标量输运大涡模拟[J]. 水利水电科技进展, 2013, 33(2): 26−31.Lu Jun, Wang Lingling, Cao Xiaohong. Large eddy simulation of jets with and without temperature scalar in a current[J]. Advances in Science and Technology of Water Resources, 2013, 33(2): 26−31. [12] 王娅娜. 波流环境下垂向射流水动力及稀释特性实验研究[D]. 南京: 河海大学, 2015. Wang Yana. Experimental study on hydrodynamics and initial dilution of a vertical jet in wavy cross-flow environment[D]. Nanjing: Hohai University, 2015. [13] Xu Zhenshan, Chen Yongping, Tao Jianfeng, et al. Three-dimensional flow structure of a non-buoyant jet in a wave-current coexisting environment[J]. Ocean Engineering, 2016, 116: 42−54. doi: 10.1016/j.oceaneng.2016.02.022 [14] Xu Zhenshan, Chen Yongping, Wang Yana, et al. Near-field dilution of a turbulent jet discharged into coastal waters: effect of regular waves[J]. Ocean Engineering, 2017, 140: 29−42. doi: 10.1016/j.oceaneng.2017.05.003 [15] Xu Zhenshan, Chen Yongping, Pan Yi. Initial dilution equations for wastewater discharge: example of non-buoyant jet in wave-following-current environment[J]. Ocean Engineering, 2018, 164: 139−147. doi: 10.1016/j.oceaneng.2018.06.021 [16] Chin D A. Model of buoyant-JET-surface-wave interaction[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 1988, 114(3): 331−345. doi: 10.1061/(ASCE)0733-950X(1988)114:3(331) [17] Jirka G H. Integral model for turbulent buoyant jets in unbounded stratified flows. Part I: single round jet[J]. Environmental Fluid Mechanics, 2004, 4(1): 1−56. doi: 10.1023/A:1025583110842 [18] 周连伟. 三维非恒定流场中圆形浮射流的数值模拟研究[D]. 大连: 大连理工大学, 2004.Zhou Lianwei. Numerical study on round buoyant jet in 3D unsteady flow[D]. Dalian: Dalian University of Technology, 2004. [19] Lin Yingpin, Hsu H C, Chen Y Y. Theoretical analysis of a buoyant jet interacting with small amplitude waves[J]. China Ocean Engineering, 2009, 23(1): 73−84. [20] 胡飞, 陈永平, 徐振山, 等. 波浪环境下垂直射流动量积分模型[J]. 水利学报, 2013, 44(9): 1058−1063, 1070.Hu Fei, Chen Yongping, Xu Zhenshan, et al. A momentum integral model for vertical jet in wavy environment[J]. Journal of Hydraulic Engineering, 2013, 44(9): 1058−1063, 1070. [21] Lai A C H, Law A W K, Adams E E. A second-order integral model for buoyant jets with background homogeneous and isotropic turbulence[J]. Journal of Fluid Mechanics, 2019, 871: 271−304. doi: 10.1017/jfm.2019.269 [22] Shrivastava I, Lai A C H, Adams E E. Numerical model for unidirectional diffuser in a crossflow[J]. Journal of Hydraulic Engineering, 2022, 148(7): 04022010. doi: 10.1061/(ASCE)HY.1943-7900.0001987 [23] He Zhiguo, Lou Yingzhong. Integral model for multiple forced plumes arranged around a circle in a linearly stratified environment[J]. Physical Review Fluids, 2019, 4(12): 123501. doi: 10.1103/PhysRevFluids.4.123501 [24] Chen Yanan, He Zhiguo, Lou Yingzhong, et al. Experimental study of horizontal heated buoyant jets in a linearly stratified ambience[J]. Physics of Fluids, 2021, 33(4): 047116. doi: 10.1063/5.0045906 [25] He Zhiguo, Zhang Han, Chen Yanan, et al. Hydrodynamics of horizontal heated buoyant jet in linearly stratified fluids[J]. Physics of Fluids, 2022, 34(2): 025108. doi: 10.1063/5.0077726 [26] 方树桥. 波流环境中射流动量积分通用模型研究及应用[D]. 南京: 河海大学, 2020. Fang Shuqiao. Study and application of general momentum integral model for a jet in wavy current environment[D]. Nanjing: Hohai University, 2020. [27] Xu Zhenshan, Chen Yongping, Jiang Dongbo. Experimental study on a buoyant jet in wavy crossflow[C]//Proceedings of the 28th International Ocean and Polar Engineering Conference. Sapporo: International Society of Offshore and Polar Engineers, 2018: 891−897. -
下载:
计量
- 文章访问数: 164
- HTML全文浏览量: 92
- PDF下载量: 28
- 被引次数: 0
