Barotropic feature of ocean striations in the North Pacific
-
摘要: 海洋中包含着多种时空尺度的运动过程，海洋带状流是近年来发现的一种新的流动形式。这种流动现象介于地转湍流和准定常流之间。上层海洋中大尺度运动的强度远大于海洋带状流而将其遮盖，因而带状流需要借助滤波方法提取出来。本研究基于纬向速度数据，通过切比雪夫高通滤波提取了北太平洋海洋带状流的三维结构，定义了“流向稳定度”指数，量化分析了北太平洋海域带状流的正压特性，从而进一步加深了对北太平洋海洋带状流结构特征的认识。Abstract: The ocean contains various spatiotemporal scales of motion processes, and ocean striations are a newly discovered form of flow in recent years. This flow phenomenon lies between geostrophic turbulence and quasi-steady flow. Due to the dominance of large-scale motion in the upper ocean, ocean striations are masked and need to be extracted using filtering methods. In this study, the three-dimensional structure of ocean striations in the North Pacific was extracted based on zonal velocity data using Chebyshev high-pass filtering. The “flow stability” index was defined to quantitatively analyze the barotropic feature of ocean striations in the North Pacific, thereby deepening the understanding of the structural characteristics of ocean striations in the North Pacific.
-
Key words:
- striations /
- the North Pacific /
- barotropy
-
1. 引言
带状流动广泛存在于自然界的流体中，从微观尺度的等离子体到宏观的行星大气都能发现该运动形式。实验中也可以模拟出带状流动，例如Read等[1]利用圆柱形储罐锥形的倾斜底部，使整个储罐获得一定的角速度，数小时后水槽中出现了一种方向交替的带状流型。过去木星大气层的条带流动结构常受到科学家的关注[2–3]。最近10多年来，物理海洋学家发现海洋中也存在带状流结构。
海洋中的带状流是指经向上流向交替组成的准纬向流，该结构在经向上为中尺度，纬向上具有海盆尺度，垂向上可以连续地延伸到深海[4]，且遍布整个海洋[5]。纬向带状流动的产生机制，过去已经提出了一些相关理论，例如，Rhines[6]提出在β效应下，二维湍流场在能量逆级串的过程中会产生一种交替的纬向急流结构；Baldwin等[7]称纬向流与位势涡度的分布密切相关，位势涡度的经向梯度较大处与狭窄、流速更快的东向流的位置相对应；Qiu等[8]提出斜压罗斯贝波的三波共振可以产生带状流动；Chen等[9]认为带状结构是涡旋传播的结果。
海洋带状流有不同的提取方法，例如，Maximenko等[10]通过二维汉宁高通滤波提取了太平洋东部的带状流；Ivanov等[11]通过小波变换提取了加利福尼亚外海的带状流动系统；Van Sebille等[12]通过高通滤波提取了东北太平洋海域内的带状流动；张宇等[13]通过一维的切比雪夫高通滤波器提取到了全球海洋条带结构。
在已发表的文献中，带状结构的描述常常采用不同的名称，例如“纬向流（zonal currents）”[14]、“准纬向急流（quasi-zonal jets）”[12]、“纬向急流（zonal jets）”[15]等。值得注意的是，海洋中的带状流在结构上与急流非常接近，都呈现出带状结构。实际上，提取到的海洋带状流比背景流场弱，而急流要比背景流场的强度强，前者的量级约为cm/s，而后者往往为m/s，两者不应混为一谈。本文将使用带状流（striations）的概念，以示其与急流（jets）的区别。
海洋带状流在垂向上呈正压结构。前人对带状流的研究也注意到了其正压结构。Richards等[16]对太平洋的研究发现，热带区域和中高纬度区域（30°～50°N）的带状结构有着明显的不同，在中高纬度带状流几乎都能从表层贯穿到底部。带状结构的垂向结构主要由正压模和前两个斜压模主导[17]。带状结构在整个深度截面上不存在明显的倾斜[18]。Van Sebille等[12]通过对多个流轴上带状流的流向的识别和统计，证明带状流具有正压性。通过对不同区域的研究，Zhang和Guan[5]认为开阔海域带状流的正压性强于边缘海等孤立海盆。前人对海洋带状流正压性的分析以描述为主，缺乏定量的研究。因此本文以北太平洋海洋带状流为研究对象，通过定义多种指数，对其正压结构进行了定量的研究。我们采用了一种新的角度“不同深度带宽的对比”并定义了一个“流向稳定度”指数来定量研究北太平洋海洋带状流的正压性。
2. 资料和方法
2.1 资料
2.1.1 SODA资料
本研究中使用由美国马里兰大学和得克萨斯农工大学合作完成的资料集SODA（Simple Ocean Data Assimilation）数据。SODA数据的版本为SODA 3.4.2（https://www2.atmos.umd.edu/~ocean/），纬度范围为74.5°S～90°N，不包含南极区域，其时间分辨率为月平均，水平分辨率为0.5° × 0.5°，垂向上分为50层，时间范围为1980−2020年。研究中使用的数据为纬向流场，因为海洋中的低频大尺度流动以纬向流为主。
2.1.2 ECCO资料
ECCO（Estimating the Circulation and Climate of the Ocean）资料属于同化数据，该资料的相关项目创立于1998年，是世界大气环流实验（World Ocean Circulation Experiment）的一部分。ECCO2（Phase II）的推出是为了改进ECCO数据的水平网格粗糙和缺少部分海区等问题。ECCO2通过使用格林函数结合多种观测数据对环流模型进行同化，拥有精细的分辨率，能再现全球范围的海洋。本研究中使用数据的时间尺度为2001−2010年，水平分辨率为0.25° × 0.25°，垂向上共有50层。
2.2 方法
2.2.1 带状流的提取——切比雪夫高通滤波方法
本研究使用切比雪夫高通滤波方法提取海洋带状流。张宇等[13]对比了高斯平滑、汉宁方法和切比雪夫3种滤波方法在海洋中得到的带状结构特征，研究结果如下：高斯平滑只能在局部区域获得带状结构，不适用于全球范围内带状流的提取；汉宁方法和切比雪夫方法的结果大致相同，可以在全部范围内提取带状结构，但汉宁方法得到的结果在纬向上相比真实位置会发生一定程度的偏移，而切比雪夫方法不存在位置偏移问题。所以本研究采用切比雪夫方法。
2.2.2 带状流的带宽算法
海洋带状流呈现为南北方向上相邻且交替反向的流动。基于这种结构特征，可以采用“几何带宽算法”计算带状流单条流带的宽度。该算法在经向上进行：第一步，找到东向或是西向流的极值点位置（流轴）；第二步，找到两个相邻且符号相反的极值点之间，流速为0的位置（东向流和西向流的边界）；最后，计算相邻两个边界之间的距离便可以得到带状流宽度。此方法存在一定的局限性，因为从带状流的空间分布上来看，宽度值较小的带状流占空间范围较小，但在统计带宽总体的分布时，宽度值不同的带状流所占权重却相同。这将导致在区域内计算带宽的平均分布状况时，获得的结果往往偏小。
针对这个不足，我们进行订正：计算出单条带状流的带宽后，将值赋值给该带状流所占空间范围内的所有格点，如图1小红圈所示。完成目标区域内所有经度上的带宽计算后，该区域内每个空间格点也都具备了带宽属性，进而能得到二维平面上的带宽分布，即与资料相同分辨率的带宽分布。订正后的带宽算法降低了带宽值较小的流动对总体带宽分布的影响，从而有效提高了整体带宽计算的准确性。
2.2.3 流向稳定度
为进一步探究各区域带状流在垂向上的分布情况，下面定义“流向稳定度”指数来描述带状流的垂向延拓特征在空间上的变化。
以SODA数据中997 m深度上的流场为例，第一步进行时间平均和滤波处理，提取海洋带状流，见图2a。第二步，将图2a中的流速分布转化为东西流向分布，流速为正值和负值的东向流和西向流分别进行赋值，得到如图2b所示的“流向图”。流向图只标记流动的方向不包含流速的大小。图2b可清晰地观察到每个格点上的流向情况，同时在流向图中能更有效地得到一定经度范围内带状流的条数信息。
图 2 基于SODA数据的北太平洋997 m深度上带状流流速（a）、流向（b）、在不同深度上流向不变和发生变化的区域（c）和流向稳定度（d）偏黄色区域表示流向在深度上稳定度较高的区域，偏蓝色区域则表示流向在深度上稳定度较低的区域Figure 2. Based on SODA data, the striations current velocity at 997 m in the North Pacific (a), flow direction (b), regions of flow direction vertically in alignment and regions where flow direction changes at different depths (c), and the stability of flow direction (d)The yellow region indicates the area where the flow direction is stable over the depth, while the blue region indicates the area where the flow direction varies over the depth第三步，将上述在单层进行的“流向图”转换扩展到1500 m内的不同深度层，继而在每一个经纬度格点上对多个深度上的流向值做比较。若在同一地理格点上，多个深度上的流速方向相同，说明流向未曾发生改变，则将该处设置为当前的流向；若有不同的流向值出现，表示该位置的流向发生了改变，便将该位置的格点设置为空值。如图2c所示，该区域东南区域的空值点比较多，这在一定程度上说明该部分区域内的带状流从浅到深的一致性较差。图2c展示的是流向在深度上的变化情况，为进一步用数值来描述流向变化的分布特征，需要在此基础上进行量化。
第四步，将流向不变的格点赋值为数值“1”，流向发生改变的格点赋值为数值“0”，设定2 × 2的4个格点为一个局部网格，在网格内进行平均，将平均值赋值给网格内的4个格点，以此，每个格点便都具有了代表流向变化的“流向稳定度”。如图2d所示，不同的颜色代表“流向稳定度”的高低，偏黄色的区域为该部分缺失数据较少，表示该区域流向在深度上的稳定度较高，相应地，偏蓝色区域则表示流向稳定度低。
2.2.4 斜压分量算法
Zhang等[4]用一个无量纲常数—斜压分量指数对带状流的正压性进行了考察，并给出了北太平洋2000 m以内的斜压分量指数变化情况。斜压分量指数可以计算流场斜压分量的比重，斜压分量指数越小表明流场的正压性越强，反之，则正压性较弱。我们进一步研究了北太平洋断面上斜压分量指数的变化情况。纬向流（
$ {u}_{0} $ ）的斜压分量指数（BCF0）可以通过下式进行定义：$$ {u}_{0,\;{\mathrm{bt}}}\left(x,y\right)=\frac{1}{d}{\int}_{ {-d}}^{0}{u}_{0}\left(x,y,z\right)\mathrm{d}z\text{，} $$ (1) $$ {u}_{0,\;{\mathrm{bc}}}\left(x,y,z\right)={u}_{0}\left(x,y,z\right)-{u}_{0,\;{\mathrm{bt}}}\left(x,y\right)\text{，} $$ (2) $$ {{\mathrm{BCF}}}_{0}=\frac{z\;\mathrm{max}({u}_{0,\;{\mathrm{bc}}})}{{u}_{0,\;{\mathrm{bt}}}+z\;\mathrm{max}({u}_{0,\;{\mathrm{bc}}})}\text{，} $$ (3) 带状流流速（
$ {u}_{{\mathrm{str}}} $ ）的斜压分量指数（$ {{\mathrm{BCF}}}_{{\mathrm{str}}} $ ）计算公式为$$ {u}_{{\mathrm{str}},\;{\mathrm{bt}}}\left(x,y\right)=\frac{1}{d}{\int }_{-d}^{0}{u}_{{\mathrm{str}}}\left(x,y,z\right)\mathrm{d}z \text{，} $$ (4) $$ {u}_{{\mathrm{str}},\;{\mathrm{bc}}}\left(x,y,z\right)={u}_{{\mathrm{str}}}\left(x,y,z\right)-{u}_{{\mathrm{str}},\;{\mathrm{bt}}}\left(x,y\right) \text{，} $$ (5) $$ {{\mathrm{BCF}}}_{{\mathrm{str}}}=\frac{z\;\mathrm{max}({u}_{{\mathrm{str}},\;{\mathrm{bc}}})}{{u}_{{\mathrm{str}},\;{\mathrm{bt}}}+z\;\mathrm{max}({u}_{{\mathrm{str}},{\mathrm{bc}}})} \text{，} $$ (6) 式中，
$ {u}_{0,\;{\mathrm{bt}}} $ 和$ {u}_{{\mathrm{str}},\;{\mathrm{bt}}} $ 表示正压分量；$ {u}_{0,\;bc} $ 和$ {u}_{{\mathrm{str}},\;{\mathrm{bc}}} $ 表示斜压分量；$ z\;\mathrm{m}\mathrm{a}\mathrm{x}({u}_{0,\;{\mathrm{bc}}}) $ 与$ z\;\mathrm{m}\mathrm{a}\mathrm{x}({u}_{{\mathrm{str}},\;{\mathrm{bc}}}) $ 分别表示垂向上流场斜压分量的最大振幅。斜压分量值可验证流动中正压和斜压的占比，该值越靠近0.5，正压和斜压分量占比越趋近，而当该值小于0.5并越接近0时，说明正压分量越占优。3. 北太平洋带状流的正压性特征
3.1 不同深度带宽的对比
提取海洋带状流首先需要对2001−2010年纬向流数据进行时间平均，然后为了去掉背景流场中ENSO和太平洋年代际震荡等大尺度过程的信号，便须对原始平均流场使用高通滤波进行处理。结果表明，北太平洋海洋带状流在等深面上纬向具有海盆尺度，经向为中尺度，与前人的结果一致[4, 10, 18]。基于SODA数据，北太平洋整体的带宽分布集中于100～200 km，其中100～200 km的带宽占比为55%。图3中自上到下分别是3种不同的经度范围内带状流宽度随纬度和深度的变化情况。图中不同颜色曲线分别代表6 m、525 m、997 m和1498 m深度上的宽度变化，以及以上4种深度整体平均的情况。图中浅灰色阴影区域为4种深度整体平均在纬度上的变化范围，虚线为该范围的边界。
图 3 基于SODA数据，带状流宽度在3个经度范围内随纬度的变化橙色，红色，紫色和银色4条细线代表4种深度上的带宽变化情况，黑色粗实线表示以上4种深度上的平均，其中3个经度范围在图4中用黑框表明Figure 3. Based on SODA data, the meridional variability of bandwidth of the striations over three longitudinal bandsThe four thin lines (orange, red, purple and silver) depict the meridional distribution of bandwidth at four depths, while the heavy black lines represent the average over these four depths. The three longitude ranges are indicated by black boxes in Fig. 4从纬向进行分析，图3a和图3b变化相似：15°～25°N之间，两个区域内的带宽整体呈变窄趋势，局部有所波动；25°～35°N之间，宽度值在波动中有缓慢的变窄；35°～40°N之间，可能受强烈的背景流场影响，条带有一定程度的加宽；40°～45°N，宽度继续变窄。图3c中，15°～30°N之间，带宽在波动中逐步变窄，30°～35°N之间的带宽较为平稳地维持在150 km附近，随后在35°～45°N之间，带宽先加宽，随后逐步变窄。由此可以看出随纬度的增加，带状流有不断变窄的趋势。
带状流的宽度不仅能用来说明带状流的尺度特征，还可以通过对比不同深度上的带宽值，获取相应位置上带状流流向随深度的变化情况。若从表层至深层的带宽相近，说明该区域带状流在垂向上流向变化小，表明流动具有一定的正压结构。从深度上进行分析，图3中所示的4种深度，在3个纬度范围内表现相近：15°～20°N处低纬度热带地区流系复杂，不同深度间带宽有所差别；超过20°N，随着纬度升高，4个深度上的带宽波动趋势相似度很高，同时也有更多区域的带宽值趋于一致。例如图4a中38°～45°N范围内的带宽在4种深度上较为接近，证明该区域范围内的带状流具有明显的正压结构。
图 4 基于SODA数据的北太平洋997 m深度上的带状流流速和流向稳定度偏黄色区域表示流向在深度上稳定的区域，偏蓝色区域则表示流向在深度上稳定度较差的区域Figure 4. Based on SODA data, the striations at current velocity at 997 m and the stability of flow direction in the North PacificThe yellow region indicates the area where the flow direction is stable over the depth, while the blue region indicates the area where the flow direction varies over the depth3.2 不同深度流向的对比
图4和图5展示了基于两种数据，北太平洋的带状流和流向稳定度的分布情况。图4基于SODA数据，流向稳定度的分布显示，北太平洋海区整体流向稳定区域较多，热带区域存在着复杂的垂向流系，如赤道潜流[19]，流场的垂向一致性较小；中纬度区域带状流流向在深度上变化较弱，垂向一致性较强，因而具有更强的正压性。
图 5 基于ECCO2数据的北太平洋1007 m深度上的带状流流速和流向稳定度偏黄色区域表示流向在深度上稳定的区域，偏蓝色区域则表示流向在深度上稳定度较差的区域Figure 5. Based on ECCO2 data, the striations at current velocity at 1 007 m and the stability of flow direction in the North PacificThe yellow region indicates the area where the flow direction is stable over the depth, while the blue region indicates the area where the flow direction varies over the depth如图5所示，基于ECCO2数据，流向稳定度的分布情况与SODA数据大致相似，北太平洋整体稳定性较强，热带区域垂向一致性较差。而两种数据也存在一处较为明显的差别，由于ECCO2数据分辨率较高，能表现出较为精细的流向稳定度的分布情况，因而在图5中，从带状流与流向稳定度分布两图中对比可以发现，尤其在热带区域，带状流的流轴位置一般流向稳定度较高。
3.3 北太平洋海洋带状流的正压性指数
图6a与图6b和图7a与图7b展示了SODA和ECCO2两种数据在北太平洋180°原始纬向平均流与带状流。图6a与图7a为原始的纬向流场，图中可见部分热带地区和中纬度区域上层的大尺度环流。纬向流场的热带地区潜层流系复杂，上层的西向流延伸至700 m深；中纬度地区的上层流场部分区域可贯穿至2 000 m。纬向流的上层涵盖了大尺度风生环流场，深层的流场开始呈现东西向交替的带状特征。图6b与图7b是经滤波得到的带状流。对比纬向流和带状流可以发现，带状流流轴处往往与纬向流的深层流的流向一致，这在一定程度上表明带状流在上层被强度更大的背景流场所掩盖，直到深层才逐渐显露出来。
图 6 SODA数据中的180°剖面的不同深度纬向流流速（a）、不同深度滤波后分离出的带状流流速（b）以及纬向流和带状流流场的斜压分量指数随纬度的变化（c）蓝色和红色的实线分别为纬向流和带状流斜压分量指数的变化，蓝色和红色的虚线则分别为两者的均值；灰色阴影部分为斜压分量指数小于0.5的区域Figure 6. Based on SODA data, zonal flow current velocity along 180° in different depths (a), striations current velocity obtained after filtering in different depths (b), and BCF index for the zonal flow and striation (c)Where the blue (red) solid line for the zonal flow (striation) BCF index, and the blue (red) dashed line for the mean values; the shaded area indicates BCF index less than 0.5
图 7 ECCO2数据中180°剖面的不同深度纬向流流速（a）、不同深度滤波后分离出的带状流流速（b）以及纬向流和带状流流场的斜压分量指数随纬度的变化（c）蓝色和红色的实线分别为纬向流和带状流斜压分量指数的变化，蓝色和红色的虚线则分别为两者的均值；灰色阴影部分为斜压分量指数小于0.5的区域Figure 7. Based on ECCO2 data, zonal flow current velocity along 180° in different depths (a), striations current velocity obtained after filtering in different depths (b), and BCF index for the zonal flow and striation (c)Where the blue (red) solid line for the zonal flow (striation) BCF index, and the blue (red) dashed line for the mean values; the shaded area indicates BCF index less than 0.5利用斜压分量指数可以计算出正压性，其中深度d取2 000 m。纬向流和带状流的斜压分量值变化情况如图6c与图7c所示。黑色虚线标注了斜压分量极小值的位置与纬向流和带状流在纬向上的对应关系。整体来看，图6与图7中纬向流的斜压分量均值为0.639与0.705，斜压分量占优；而带状流中斜压分量平均值为0.536与0.565。可见，相比纬向流场，带状流流场具有更强的正压性。从单个带状流来看，带状流流轴位置常常是斜压分量极小值位置，而流动的边界位置处斜压分量指数较高，证明带状流流轴位置附近的正压性较强。带状流由纬向交替的流动组成，流轴位置处具有的较强的正压性使得流场的平均斜压分量值较低，进而证明了带状流所具有的正压性。
利用 SODA 1980−2020年的数据，可以计算出平均斜压分量指数的年份变化。图8为北太平洋原始流场和带状流流场180°断面整体平均后的斜压分量指数的变化情况，数据处理过程中同样采用了10年平均，因而横坐标为起始年份。图中可以看出原始流场的斜压分量指数在0.62～0.66之间波动，而带状流的斜压分量指数在0.51～0.57之间波动，表明了带状流在多个年份上都表现出了较强的正压特性。
图 8 SODA数据中180°断面上的多年平均斜压分量指数的变化Figure 8. Based on SODA, the change of mean BCF index over many years along 180°4. 结果与讨论
本文基于水平分辨率为0.5° × 0.5°的SODA和0.25° × 0.25° ECCO2两种数据，利用切比雪夫高通滤波提取了北太平洋带状流。通过定义带宽、流向稳定度以及斜压分量指数系统地对带状流的正压性特征进行了量化分析。结果表明：
（1）通过带宽算法定量分析了不同纬度和深度上带宽的分布特征，结果表明北太平洋海区的带宽随纬度的增加有下降趋势，且具有明显的正压结构。
（2）基于流向在深度上的变化特征，定义了“流向稳定度”指数，从不同深度上流向变化的角度研究了其正压性。该指数表明了北太平洋东部和西部的部分低纬地区，流向的稳定性较差；而北太平洋中高纬度区域、沿岸区域的稳定性较强，正压性较强，而且该区域的带宽也随深度变化较小。
（3）基于斜压分量指数分析了纬向流和带状流在垂向断面上的对应关系，结果表明带状流垂向流轴处的正压性总是强于原始的纬向流场。
强正压性反映了带状流仍是β效应下二维湍流运动的一种典型过程，是湍流各向异性化的产物，它在地球海洋中呈现出了潜藏性（表层需要滤波来提取带状流）、偏移性（水平走向与纬线不平行）等非典型的特征。带状流的斜压分量指数显著小于平均流，意味着带状流具有比海盆尺度环流场更强的正压性。而其他非典型的特征则是由于风生流动在陆地侧边界的影响下形成的海盆尺度环流场，掩盖了地转湍流成带化的结果。而且，两者之间的相互作用过程（海盆尺度与中尺度之间的相互作用）也诱导了海洋带状流的走向偏移等异化现象。海洋是显著层化的流体，带状流的正压性则体现了不同密度层流体运动的共性。这种共性必然也在整个环流场的物质和能量平衡中扮演着重要的角色，也是我们未来需要弄清的问题。此外，本文所采用的SODA数据与ECCO2数据都是同化资料，对于研究海洋带状流而言，1000 m以深实测资料仍相对较少。所以从中诊断出的带状流在深海的特征是否源于模式产生的则有待于观测资料的充分积累才能进一步地验证。
-
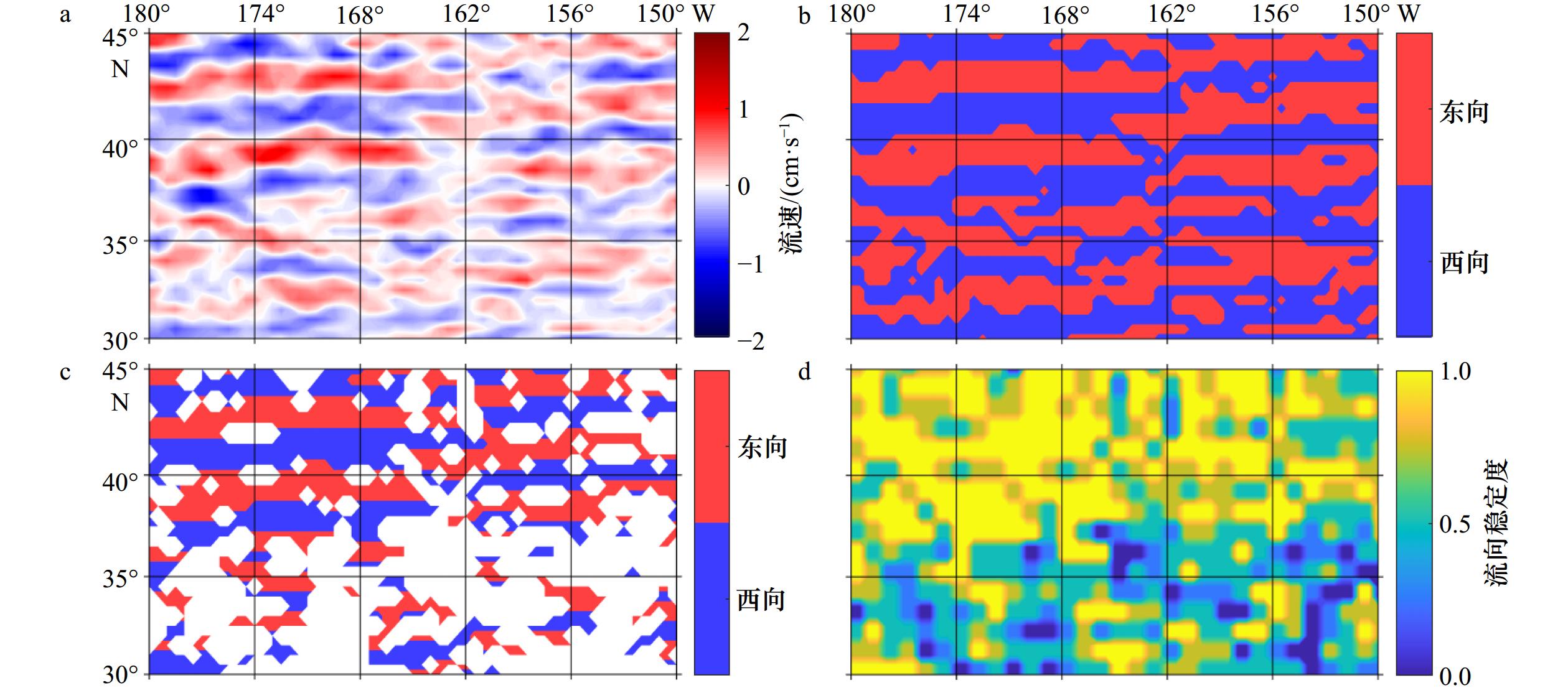
图 2 基于SODA数据的北太平洋997 m深度上带状流流速（a）、流向（b）、在不同深度上流向不变和发生变化的区域（c）和流向稳定度（d）
偏黄色区域表示流向在深度上稳定度较高的区域，偏蓝色区域则表示流向在深度上稳定度较低的区域
Fig. 2 Based on SODA data, the striations current velocity at 997 m in the North Pacific (a), flow direction (b), regions of flow direction vertically in alignment and regions where flow direction changes at different depths (c), and the stability of flow direction (d)
The yellow region indicates the area where the flow direction is stable over the depth, while the blue region indicates the area where the flow direction varies over the depth
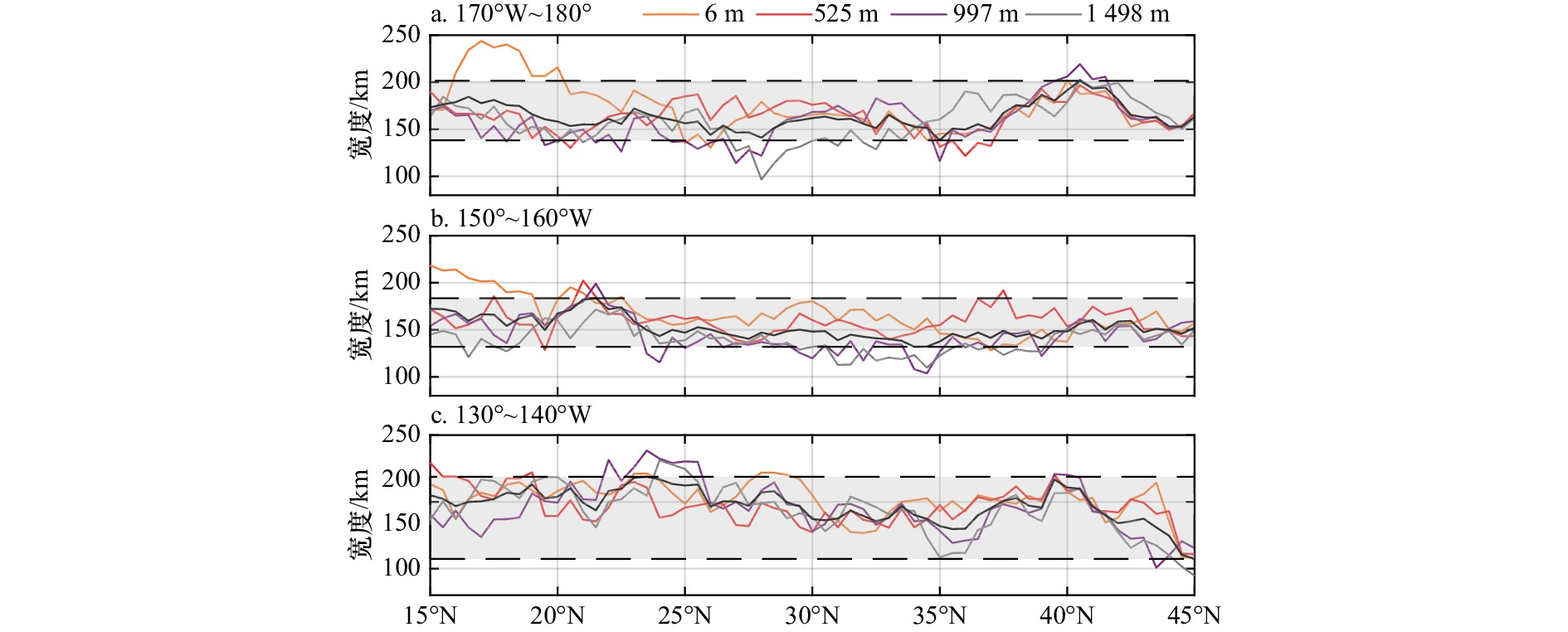
图 3 基于SODA数据，带状流宽度在3个经度范围内随纬度的变化
橙色，红色，紫色和银色4条细线代表4种深度上的带宽变化情况，黑色粗实线表示以上4种深度上的平均，其中3个经度范围在图4中用黑框表明
Fig. 3 Based on SODA data, the meridional variability of bandwidth of the striations over three longitudinal bands
The four thin lines (orange, red, purple and silver) depict the meridional distribution of bandwidth at four depths, while the heavy black lines represent the average over these four depths. The three longitude ranges are indicated by black boxes in Fig. 4
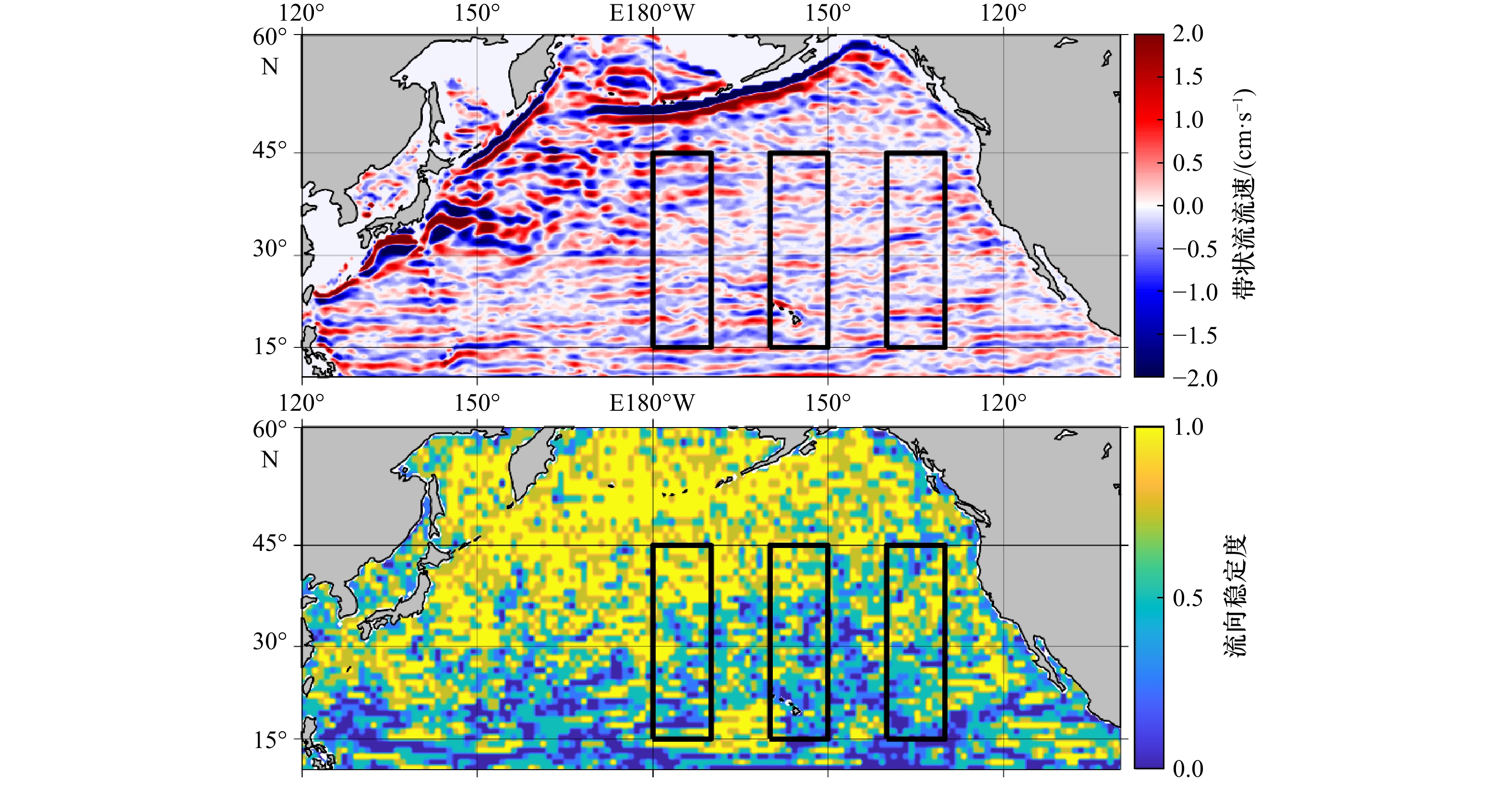
图 4 基于SODA数据的北太平洋997 m深度上的带状流流速和流向稳定度
偏黄色区域表示流向在深度上稳定的区域，偏蓝色区域则表示流向在深度上稳定度较差的区域
Fig. 4 Based on SODA data, the striations at current velocity at 997 m and the stability of flow direction in the North Pacific
The yellow region indicates the area where the flow direction is stable over the depth, while the blue region indicates the area where the flow direction varies over the depth
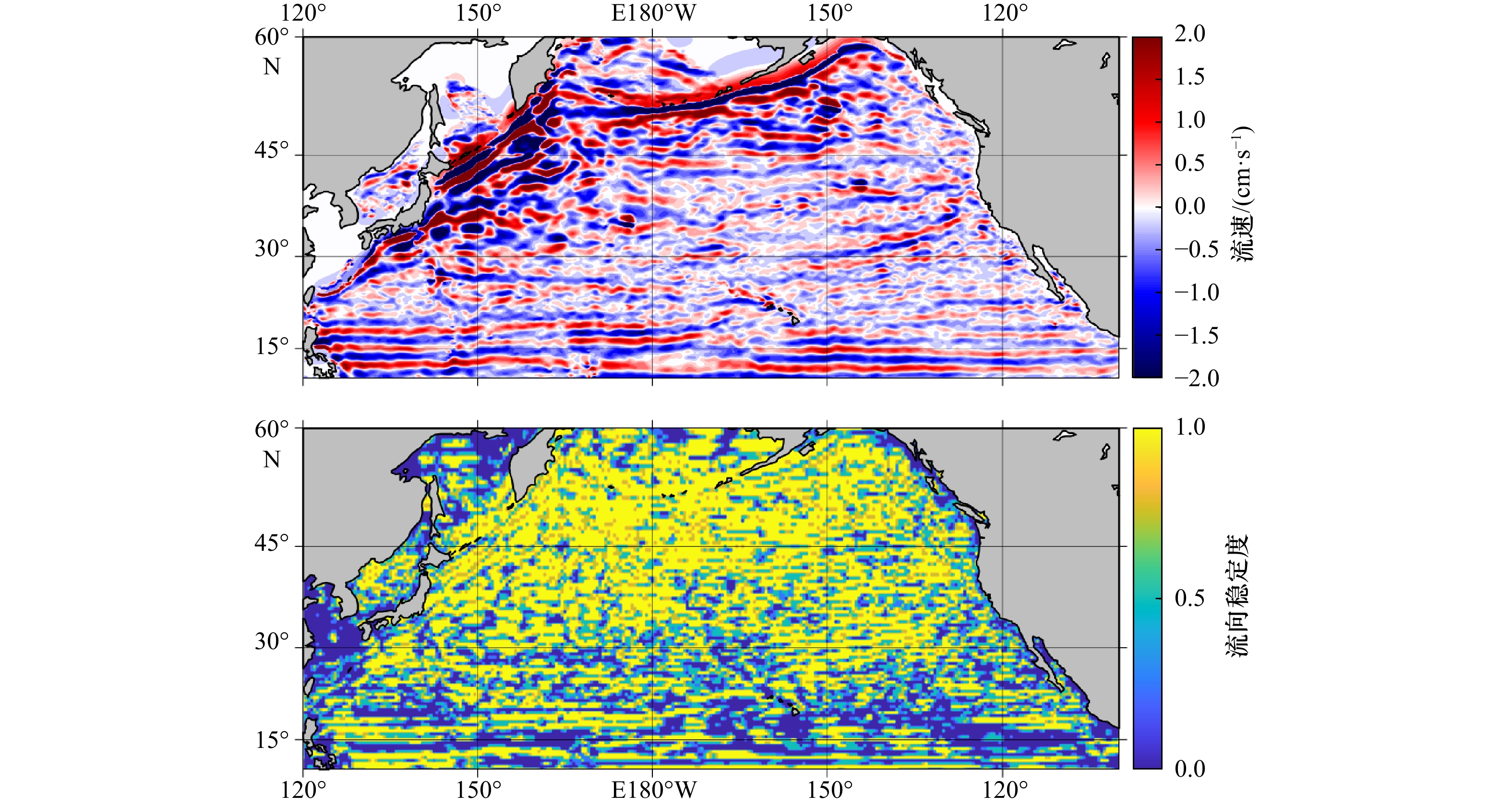
图 5 基于ECCO2数据的北太平洋1007 m深度上的带状流流速和流向稳定度
偏黄色区域表示流向在深度上稳定的区域，偏蓝色区域则表示流向在深度上稳定度较差的区域
Fig. 5 Based on ECCO2 data, the striations at current velocity at 1 007 m and the stability of flow direction in the North Pacific
The yellow region indicates the area where the flow direction is stable over the depth, while the blue region indicates the area where the flow direction varies over the depth
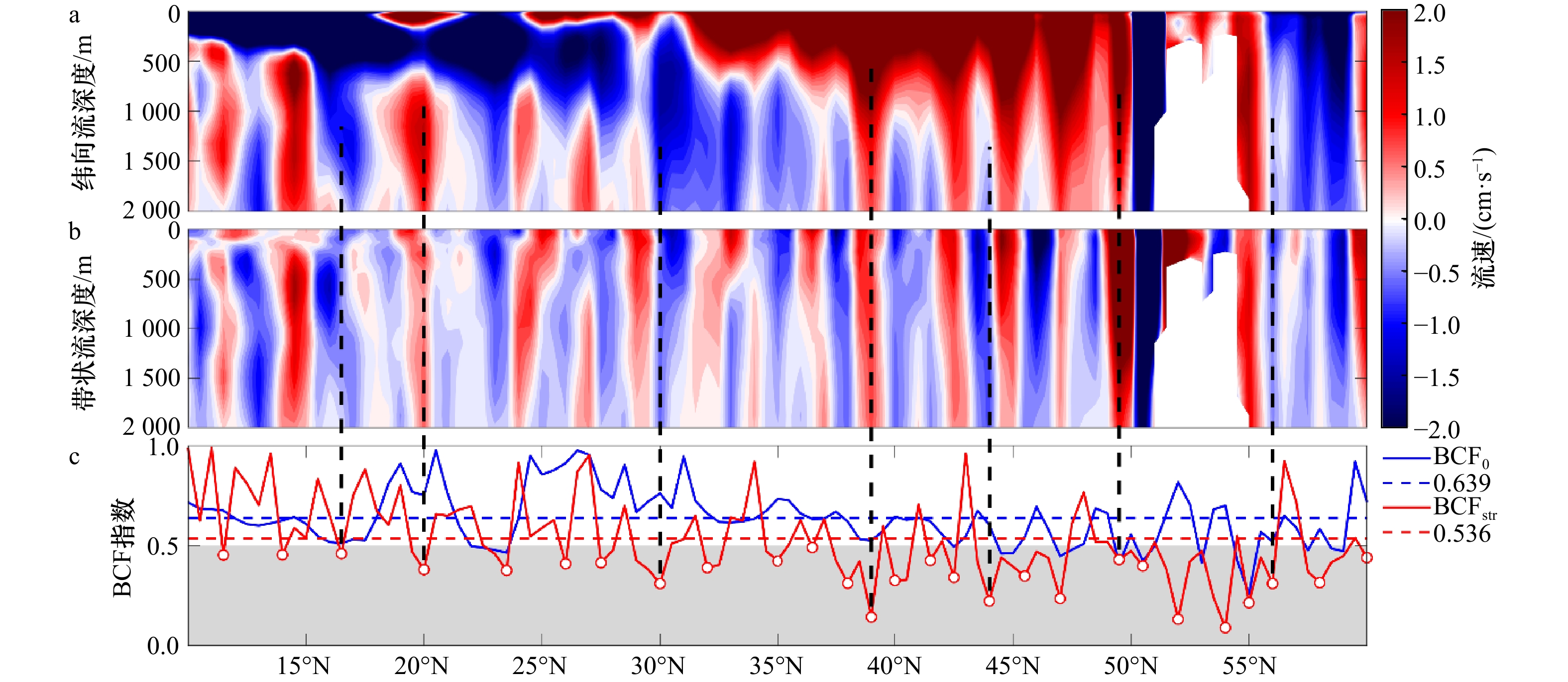
图 6 SODA数据中的180°剖面的不同深度纬向流流速（a）、不同深度滤波后分离出的带状流流速（b）以及纬向流和带状流流场的斜压分量指数随纬度的变化（c）
蓝色和红色的实线分别为纬向流和带状流斜压分量指数的变化，蓝色和红色的虚线则分别为两者的均值；灰色阴影部分为斜压分量指数小于0.5的区域
Fig. 6 Based on SODA data, zonal flow current velocity along 180° in different depths (a), striations current velocity obtained after filtering in different depths (b), and BCF index for the zonal flow and striation (c)
Where the blue (red) solid line for the zonal flow (striation) BCF index, and the blue (red) dashed line for the mean values; the shaded area indicates BCF index less than 0.5
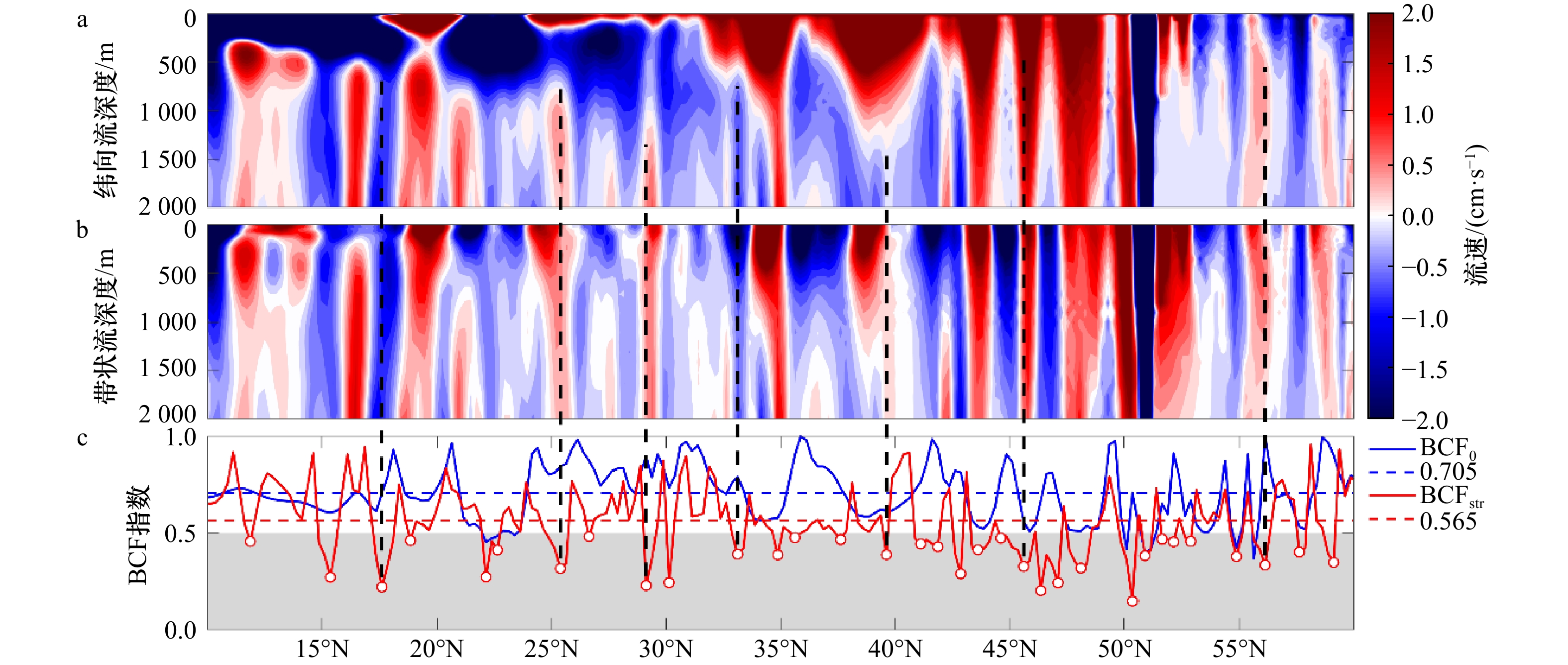
图 7 ECCO2数据中180°剖面的不同深度纬向流流速（a）、不同深度滤波后分离出的带状流流速（b）以及纬向流和带状流流场的斜压分量指数随纬度的变化（c）
蓝色和红色的实线分别为纬向流和带状流斜压分量指数的变化，蓝色和红色的虚线则分别为两者的均值；灰色阴影部分为斜压分量指数小于0.5的区域
Fig. 7 Based on ECCO2 data, zonal flow current velocity along 180° in different depths (a), striations current velocity obtained after filtering in different depths (b), and BCF index for the zonal flow and striation (c)
Where the blue (red) solid line for the zonal flow (striation) BCF index, and the blue (red) dashed line for the mean values; the shaded area indicates BCF index less than 0.5
-
[1] Read P L, Yamazaki Y H, Lewis S R, et al. Dynamics of convectively driven banded jets in the laboratory[J]. Journal of the Atmospheric Sciences, 2007, 64(11): 4031−4052. doi: 10.1175/2007JAS2219.1 [2] Galperin B, Young R M B, Sukoriansky S, et al. Cassini observations reveal a regime of zonostrophic macroturbulence on Jupiter[J]. Icarus, 2014, 229: 295−320. doi: 10.1016/j.icarus.2013.08.030 [3] Vasavada A R, Showman A P. Jovian atmospheric dynamics: an update after Galileo and Cassini[J]. Reports on Progress in Physics, 2005, 68(8): 1935−1996. doi: 10.1088/0034-4885/68/8/R06 [4] Zhang Yu, Guan Yuping, Huang Ruixin. 3D structure of striations in the North Pacific[J]. Journal of Physical Oceanography, 2021, 51(12): 3651−3662. doi: 10.1175/JPO-D-21-0076.1 [5] Zhang Yu, Guan Yuping. Striations in marginal seas and the mediterranean sea[J]. Geophysical Research Letters, 2019, 46(5): 2726−2733. doi: 10.1029/2018GL081050 [6] Rhines P B. Waves and turbulence on a beta-plane[J]. Journal of Fluid Mechanics, 1975, 69(3): 417−443. doi: 10.1017/S0022112075001504 [7] Baldwin M P, Rhines P B, Huang H P, et al. The jet-stream conundrum[J]. Science, 2007, 315(5811): 467−468. [8] Qiu Bo, Chen Shuiming, Sasaki H. Generation of the North equatorial undercurrent jets by triad baroclinic rossby wave interactions[J]. Journal of Physical Oceanography, 2013, 43(12): 2682−2698. doi: 10.1175/JPO-D-13-099.1 [9] Chen Changheng, Kamenkovich I, Berloff P. Eddy trains and striations in quasigeostrophic simulations and the ocean[J]. Journal of Physical Oceanography, 2016, 46(9): 2807−2825. doi: 10.1175/JPO-D-16-0066.1 [10] Maximenko N A, Melnichenko O V, Niiler P P, et al. Stationary mesoscale jet-like features in the ocean[J]. Geophysical Research Letters, 2008, 35(8): L08603. [11] Ivanov L M, Collins C A, Margolina T M. System of quasi-zonal jets off California revealed from satellite altimetry[J]. Geophysical Research Letters, 2009, 36(3): L03609. [12] Van Sebille E, Kamenkovich I, Willis J K. Quasi-zonal jets in 3-D Argo data of the Northeast Atlantic[J]. Geophysical Research Letters, 2011, 38(2): L02606. [13] 张宇, 管玉平, 陈朝晖, 等. 不同滤波方法对揭示全球海洋条带结构的比较[J]. 物理学报, 2015, 64(14): 149201. doi: 10.7498/aps.64.149201Zhang Yu, Guan Yuping, Chen Zhaohui, et al. Intercomparison of one-dimensional detecting methods of unveiling the global ocean striations[J]. Acta Physica Sinica, 2015, 64(14): 149201. doi: 10.7498/aps.64.149201 [14] Maximenko N A, Bang B, Sasaki H. Observational evidence of alternating zonal jets in the world ocean[J]. Geophysical Research Letters, 2005, 32(12): L12607. [15] Furue R, Nonaka M, Sasaki H. On the statistics of the zonal jets in the eastern equatorial Pacific and eastern North Pacific in an ensemble of eddy-resolving ocean general circulation model runs[J]. Ocean Modelling, 2021, 159: 101761. doi: 10.1016/j.ocemod.2021.101761 [16] Richards K J, Maximenko N A, Bryan F O, et al. Zonal jets in the Pacific Ocean[J]. Geophysical Research Letters, 2006, 33(3): L03605. [17] Kamenkovich I, Berloff P, Pedlosky J. Role of eddy forcing in the dynamics of multiple zonal jets in a model of the North Atlantic[J]. Journal of Physical Oceanography, 2009, 39(6): 1361−1379. doi: 10.1175/2008JPO4096.1 [18] Melnichenko O V, Maximenko N A, Schneider N, et al. Quasi-stationary striations in basin-scale oceanic circulation: vorticity balance from observations and eddy-resolving model[J]. Ocean Dynamics, 2010, 60(3): 653−666. [19] Cravatte S, Kestenare E, Marin F, et al. Subthermocline and intermediate zonal currents in the tropical Pacific Ocean: paths and vertical structure[J]. Journal of Physical Oceanography, 2017, 47(9): 2305−2324. doi: 10.1175/JPO-D-17-0043.1 -
下载:
下载:
计量
- 文章访问数: 420
- HTML全文浏览量: 205
- PDF下载量: 73
- 被引次数: 0
