Seasonal variation of mesoscale eddies in the Andaman Sea
-
摘要: 利用 AVISO 提供的中尺度涡数据集,对1993–2019年间安达曼海中尺度涡的涡旋特征、运动规律及其季节变化机制进行统计分析。结果显示,27年间安达曼海共出现中尺度涡328个,其中反气旋涡(171个)多于气旋涡(157个),主要分布在中西部盆地深水区。涡旋平均寿命为46.4 d,平均半径为111.8 km,平均振幅为4.7 cm,平均最大转速为24.8 cm/s,平均移动速度为15.0 cm/s,反气旋涡的平均半径、振幅和转速均大于气旋涡,而移动速度小于气旋涡。涡旋的半径、振幅和最大转速在其生命周期中都经历了先增大后减小的过程,移动速度则先减小后增大。在季节变化方面,反气旋涡和气旋涡性质冬夏对比呈现“跷跷板”现象,即夏季气旋涡比反气旋涡更多更强更大,冬季则反气旋涡更多更强更大;涡旋分布位置,夏季从北向南呈“气旋–反气旋–气旋”的极性反转交替分布,冬季则与之相反。动力机制分析显示,背景流场涡度可能影响安达曼海涡旋极性交替分布,正(负)涡度背景流利于气旋(反气旋)涡存在。涡旋能量变化机制显示,风强迫是安达曼海涡旋主要能量来源,风场能量输入与涡旋动能的季节变化吻合。Abstract: Using mesoscale eddy trajectory product from 1993 to 2019 provided by the AVISO, this study analyzes the climatology characteristics and seasonal variations of mesoscale eddies in the Andaman Sea (AS). The results show that a total of 328 mesoscale eddies were generated in the AS during the past 27 years, of which anticyclonic eddies (AEs) (171) were more than cyclonic eddies (CEs) (157). The eddies are mainly distributed in the deep waters of the central and western basin of the AS. The average life span of total eddies is 46.4 days, with average eddy radius of 111.8 km, average amplitude of 4.7 cm, rotating and propagating speeds of 24.8 cm/s and 15.0 cm/s, respectively. The AEs have large radius, amplitude, and rotating speed than CEs, but smaller propagating speed. During the eddy life, the composite radius, amplitude, and rotating speed of eddies all increase in the generation stage and then decrease in dissipation stage, while the eddy propagation speed has opposite trend. For the seasonal variation, the comparison of AEs to CEs shows seesaw phenomena in winter and summer, CEs are stronger and larger than AEs in summer, but weaker and smaller in winter. The distribution of AEs and CEs also shows seasonal polarity reversal, a ‘CEs-AEs-CEs’ pattern from north to south in summer, but a reversed ‘AEs-CEs-AEs’ pattern in winter. Dynamic analysis showed that the vorticity of background current may affect the alternating distribution pattern of mesoscale eddies in the AS, in which positive (negative) vorticity favors CEs (AEs). The energy analysis shows that wind forcing is dominant in the eddy kinetic energy (EKE) variation, and the seasonal wind work is coherent to the EKE variation in the AS.
-
1. 引言
海洋中尺度涡是全球海洋中普遍存在的中尺度现象[1],其能量通常比背景流场高出一个量级甚至更多[2]。中尺度涡在海洋动力环境[3]、物质能量输运[4]、生物化学过程[5]、全球气候变化[6]等中扮演关键角色,对海上航行和水下通信等[7]也具有重要影响,具有重要的科学研究意义和应用价值[8]。
作为海上丝绸之路的重要海域,东印度洋边缘海的中尺度涡得到学者关注。早期,Babu等[9]利用水文资料分析发现夏季在孟加拉湾西北部次表层存在一个冷涡,并认为孟加拉湾沿西边界反向流产生的斜压不稳定是冷涡形成的原因。Sanilkumar等[10]利用1993年3月水文调查资料,指出在孟加拉湾西边界的中部海域存在一个半径约为200 km的气旋涡。随着卫星遥感技术的发展,研究者基于卫星高度计产品开展中尺度涡统计分析[11-13]。Chen等[14]利用18 a卫星高度计融合数据,综合分析了孟加拉湾中尺度涡的年际变化,指出孟加拉湾涡旋活动与背景流场的斜压不稳定在年际变化尺度上的变化密切相关。Cui等[15]利用22 a的卫星高度计资料分析发现,气旋涡主要分布在孟加拉湾西北部和南部,反气旋涡主要分布在孟加拉湾东部。并且,涡旋的发生具有明显的季节变化,春季气旋涡较多,而夏季反气旋涡较多。近期,常景龙等[16]采用AVISO提供的最新中尺度涡数据集,分析了孟加拉湾1993–2016年中尺度涡的总体特征和季节变化。研究显示,孟加拉湾共发现1 553个中尺度涡,其中,孟加拉湾北部海域(15°N以北)和安达曼海是中尺度涡频发海区;涡旋生命周期主要为 28~59 d,平均振幅为7.5 cm,平均半径为119.6 km;生命周期较长(>60 d)的孟加拉湾中尺度涡具有明显的季节变化。黄挺等[17]利用1993–2017年卫星高度计数据分析了孟加拉湾及周边海域涡旋的冬夏差异,指出孟加拉湾西部、安达曼海和孟加拉湾通往赤道的出口处3个区域涡旋活动存在显著的季节性差异。
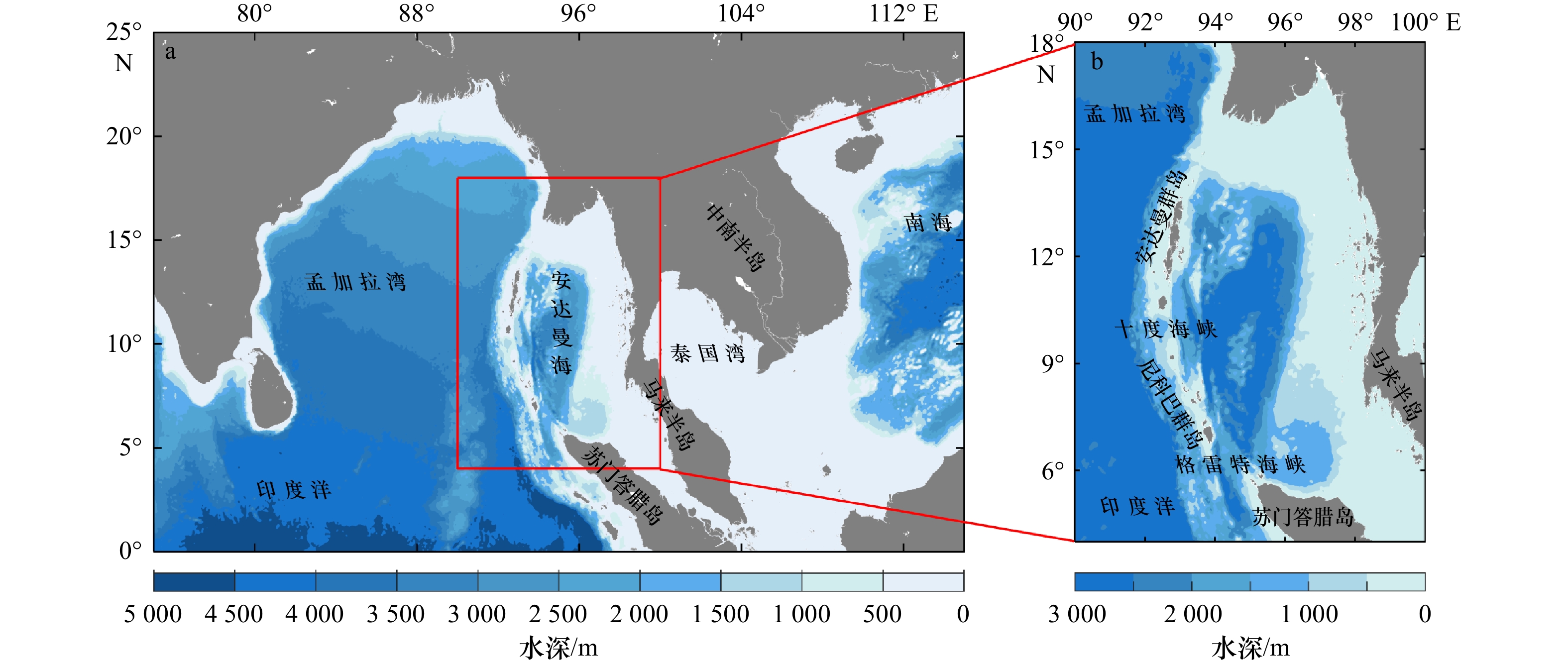
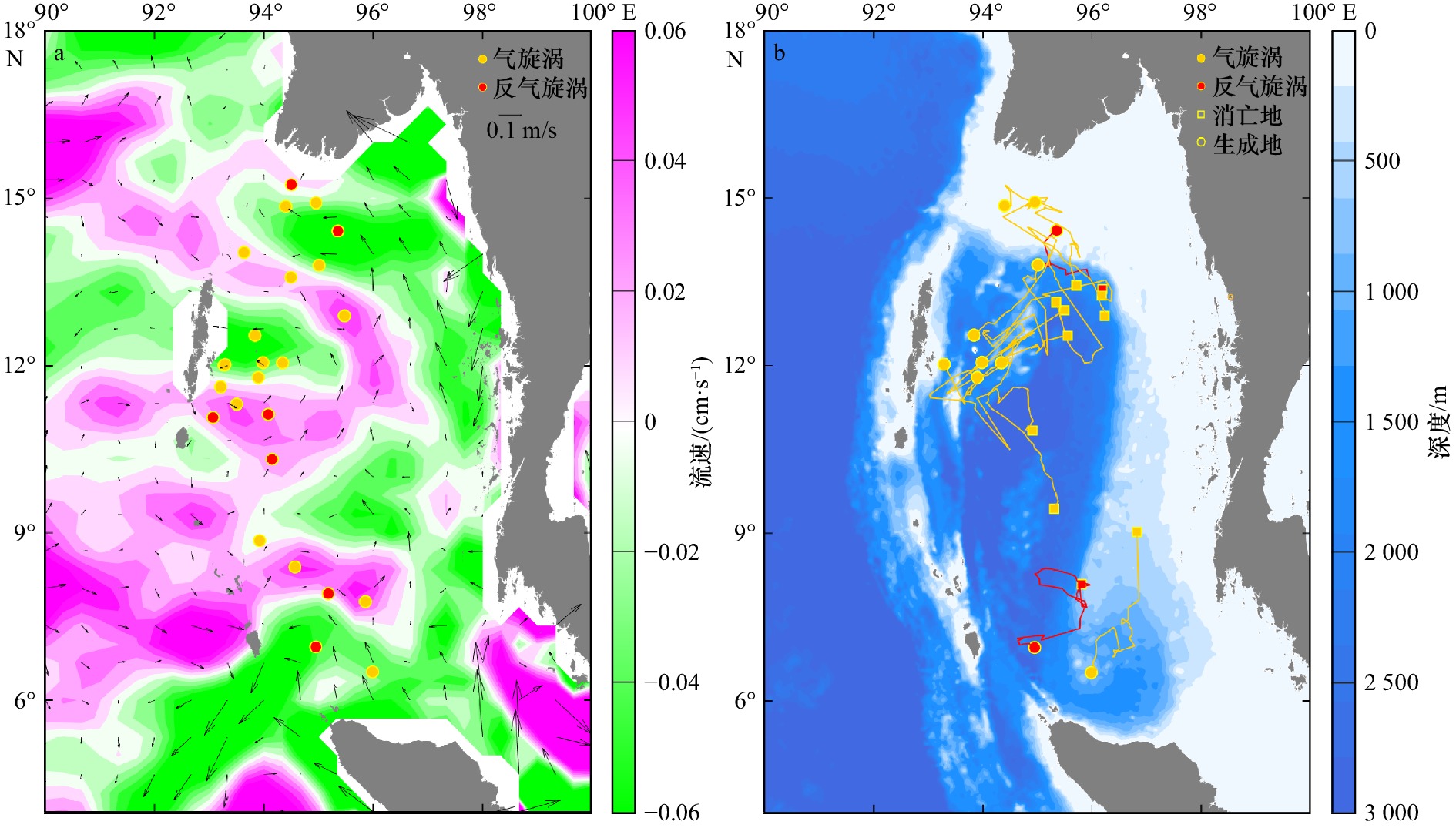
安达曼海是印度洋东北部的边缘海(图1a),西以十度海峡和格雷特海峡通印度洋,东南以马六甲海峡通南海,是南海通向印度洋的重要通道之一,也是我国海上运输和21世纪海上丝绸之路航线的关键海域[18]。海盆东浅西深,东北部陆架水深小于200 m且变化平缓,西南部为深海盆,最深处可达4 500 m(图1b)。前人研究[15-17]显示,安达曼海是中尺度涡旋活跃的海区。相比于孟加拉湾,安达曼海中尺度涡的系统研究还比较缺少。认识该海域中尺度涡的变化规律和机制有助于开展海上航行和水下通信等活动。同时,安达曼海海盆较窄(东西宽约600 km),海盆模态约束下中尺度涡特征如何,值得探究。
为此,本文将利用法国AVISO(Archiving, Validation and Interpolation of Satellite Oceanographic Data)提供的近27年的中尺度涡数据集,对安达曼海中尺度涡的数量、寿命、半径、振幅、转速、移速等涡旋特征进行统计分析,探究其空间分布以及季节变化规律,并结合背景流场和风场特征,分析安达曼海涡旋生成和变化的调控机制。本研究将加深人们对该区域中尺度涡的系统认知,提高该区域季节变化规律的认知,促进对该区域能量变化的了解。
2. 数据与方法
2.1 数据来源
本研究采用法国AVISO中尺度涡数据产品(merged delayed-time version 2.0exp),数据集的时间跨度为1993年1月1日至2020 年3月7日,该数据包含中尺度涡的位置(纬度和经度)、极性、寿命、振幅、半径、旋转速度等涡旋特征信息。该产品中的涡旋是通过生长方法识别的。该涡旋识别算法的主要原理是:先搜索海表面高度(SSH)的局部极大值(极小值)点并作为阈值的初始值,以此点为基础不断减小阈值(阈值变化间隔为0.25 cm),如果其相邻网格的SSH数值高于(低于)该阈值,则找到反气旋涡(气旋涡),涡旋网格数不断增加直到不能满足下面5个标准的任何一条为止。这5个标准包括:(1)涡旋内网格点数n≤nmax(指定的最大数);(2)n≥2,即一个涡旋中至少有两个内部格点;(3)涡旋内的所有格点的邻近格点均不属于其他涡旋;(4)涡旋中的格点是单联通的,即涡旋内没有“洞”;(5)闭合曲线内任意格点之间的距离不能超过给定的阈值dmax。对于AVISO的SSH数据,nmax取2 000。在纬度大于25°的区域内,dmax≤400 km,而在纬度小于25°的区域内,dmax≤700 km。另外,涡旋的振幅不小于 1 cm,生命周期必须在 4 周以上。有关检测算法的详细信息,可见文献[19]。
安达曼海及其邻近海域(4°~18°N,90°~100°E)地形图数据资料来源于由美国国家地球物理中心(U.S. National Geophysical Data Center, NGDC)发布的ETOPO1(https://www.ngdc.noaa.gov/mgg/global/global.html)地形资料数据。ETOPO1数据包含全球地形和海水深度数据,空间分辨率为1′。
表层流场采用美国国家海洋和大气管理局(National Oceanic and Atmospheric Administration, NOAA)的OSCAR表层流场资料,该数据是利用卫星高度计数据、海面风场资料和海面温度估算所得,时间分辨率为5 d,水平分辨率为0.33°×0.33°,时间跨度为1993年1月1日至2019年12月26日。
流场数据来源于哥白尼海洋环境监测服务(Copernicus Marine Environment Monitoring Service, CMEMS)的全球海洋集成再分析数据(GLOBAL_REANALYSIS_PHY_001_031)。该数据集时间跨度为1993年1月至2019年12月,时间分辨率为月平均,空间水平分辨率为0.25°×0.25°,垂向分辨率为75层。
地转异常流数据也采用CMEMS提供的全球海洋网格L4海面高度和衍生变量再处理数据(SEALEVEL_GLO_PHY_L4_MY_008_047)。该数据包含海表面高度、地转流速和地转异常流速,时间跨度为1993年1月1日至2019年12月31日,时间分辨率为1 d,空间水平分辨率为0.25°×0.25°。
风场数据来自欧洲中期天气预报中心(European Centre for Medium-Range Weather Forecasts,ECMWF)提供的ERA5月平均再分析数据,风场取海表面10 m处的经向和纬向分量,时间跨度为1993年1月至2019年12月,空间分辨率为0.25°×0.25°。
2.2 数据处理
分别将1993–2019年的OSCAR表层流场资料和CMEMS地转异常流数据进行月平均处理,再计算出安达曼海表层气候态季节平均流场以及气候态地转异常流场,其中,春季为3–5月、夏季为6–8月、秋季为9–11月、冬季则为12月至翌年2月。海面涡度
$ {\zeta } $ 和涡动能EKE分别由表层季节平均流场和地转异常流场计算所得,计算公式为$$ \zeta =\nabla \times {{\boldsymbol{V}}}=\frac{\partial V}{\partial x}-\frac{\partial U}{\partial y}, $$ (1) $$ {\rm{EKE}}=\frac{1}{2}\left(u'^{2}+v'^{2}\right)\text{,}$$ (2) 式中,U为海表流速的纬向分量;V为经向分量;
$ u' $ 和$ v' $ 分别为纬向地转流异常和经向地转流异常。使用相同的方法计算季节平均风场,季节风应力旋度通过
$\nabla \times {{\boldsymbol{\tau}} }$ 计算得到。风应力${{\boldsymbol{\tau}} }$ 的计算公式为$$ {\tau }={\rho }_{{\rm{air}}}{{{C}}}_{{\rm{d}}}\left|{{\boldsymbol{U}}}-{{\boldsymbol{v}}}\right|\left({{\boldsymbol{U}}}-{{\boldsymbol{v}}}\right), $$ (3) 式中,
$ {\rho }_{{\rm{air}}} $ 为大气密度(${\rho }_{{\rm{air}}}=1.25\;\mathrm{k}\mathrm{g}/{\mathrm{m}}^{3}$ );Cd为阻力系数(Cd=2.18×10-3);${{\boldsymbol{U}}}$ 和${{\boldsymbol{v}}} $ 分别为10 m处的风速和海表面流速。3. 涡旋气候态统计特征
选取生成位置在5°~18°N,92.25°~99°E范围,安达曼−尼科巴群岛东侧的涡旋为此次研究的样本。研究区27 年(1993–2019年)间共探测到15 207个涡旋,包括7 767个反气旋涡(AE)和7 440个气旋涡(CE),寿命超过28 d的涡旋分别为171个和157个,反气旋涡数量多于气旋涡。本文将针对这些涡旋进行统计分析。
3.1 涡旋生成和消亡
3.1.1 空间分布
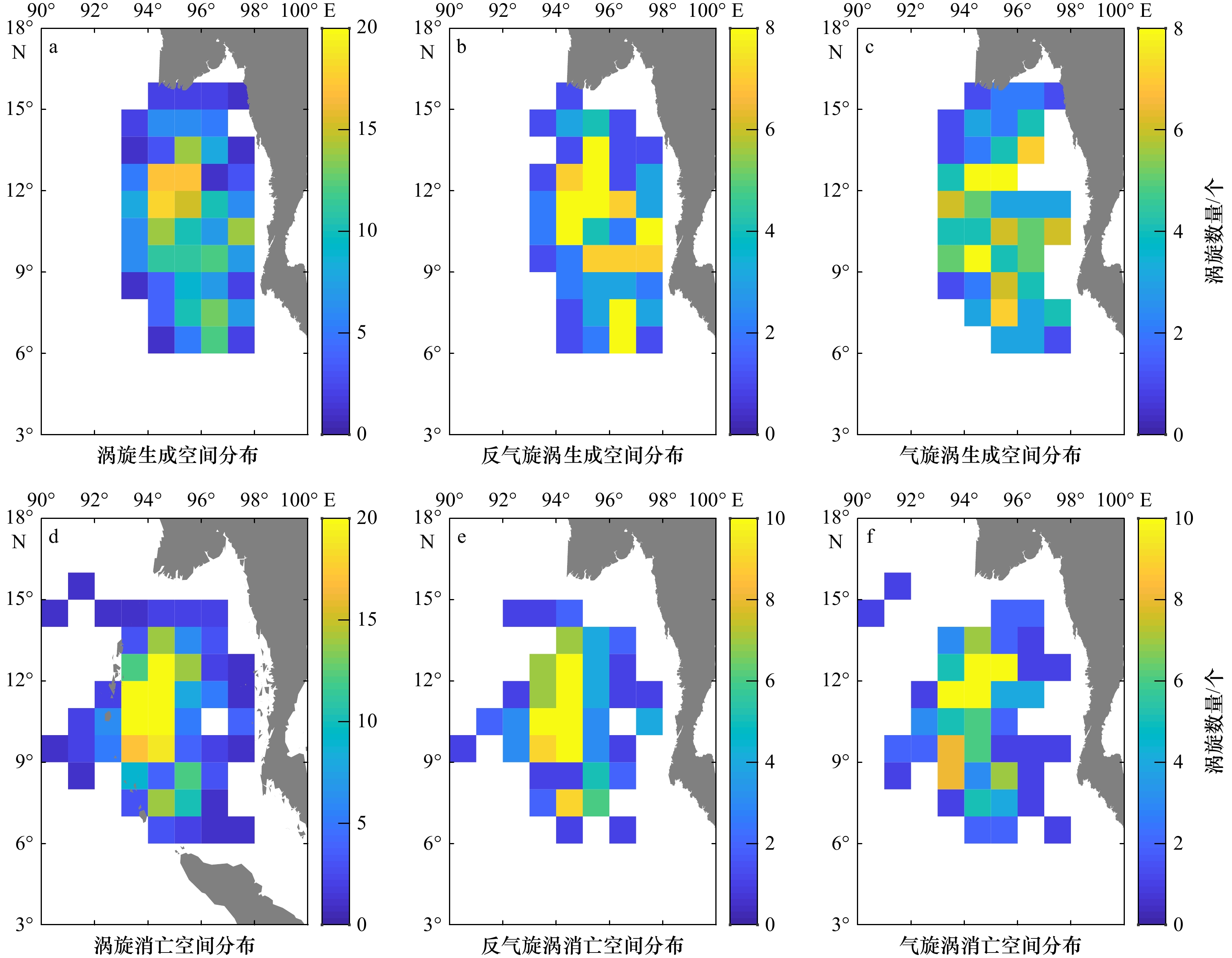
采用Chen等[20]划分网格方法,把中尺度涡生成和消亡位置细分到1°×1°的网格内,得到安达曼海中尺度涡生成和消亡个数的空间分布。如图2a所示,安达曼海内中尺度涡主要在海盆中北部生成,网格内最大生成数量为18个(年均0.6个),位于12°~13°N,95°~96°E位置。图2b和图2c分别显示出反气旋涡与气旋涡的生成位置空间分布。可见,安达曼海北部海域(13°N以北),反气旋涡生成数量比气旋涡少(数量比为23∶30),而中部(9°~13°N)则与之相反,反气旋涡生成数量明显比气旋涡生成数量多(数量比为108∶90)。从局部海域看,苏门答腊岛以北和马来半岛附近海域,反气旋涡生成频繁,而气旋涡数量较少。
图2d到图2f分别显示出总涡旋、反气旋涡与气旋涡的消亡空间分布。可见,涡旋大都消亡于海盆西部安达曼群岛附近,部分涡旋进入东印度洋深水区。对比涡旋生成(图2a),可见安达曼海中尺度涡生成后会向西传播并在西边界耗散(图2d)。反气旋涡和气旋涡均在安达曼海中部海域及安达曼群岛以东的海域消散。
3.1.2 涡旋寿命和传播距离
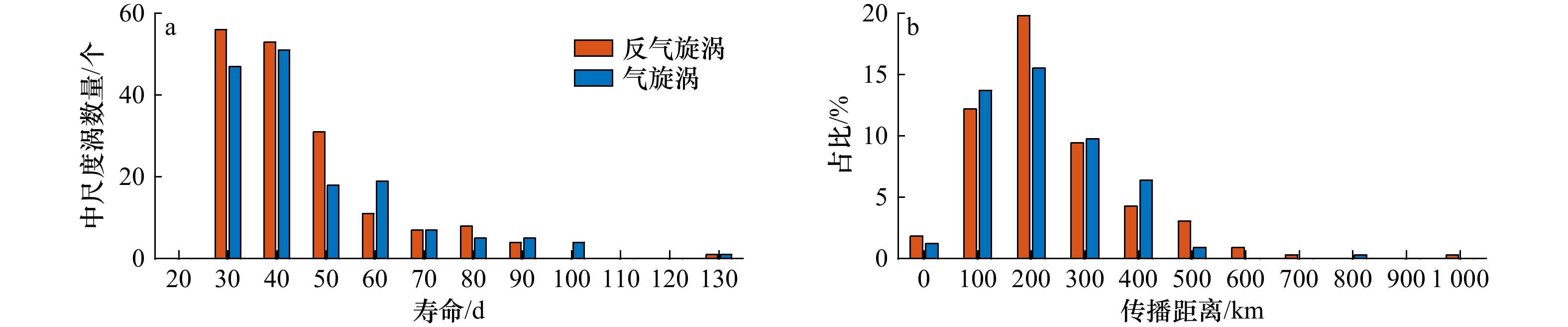
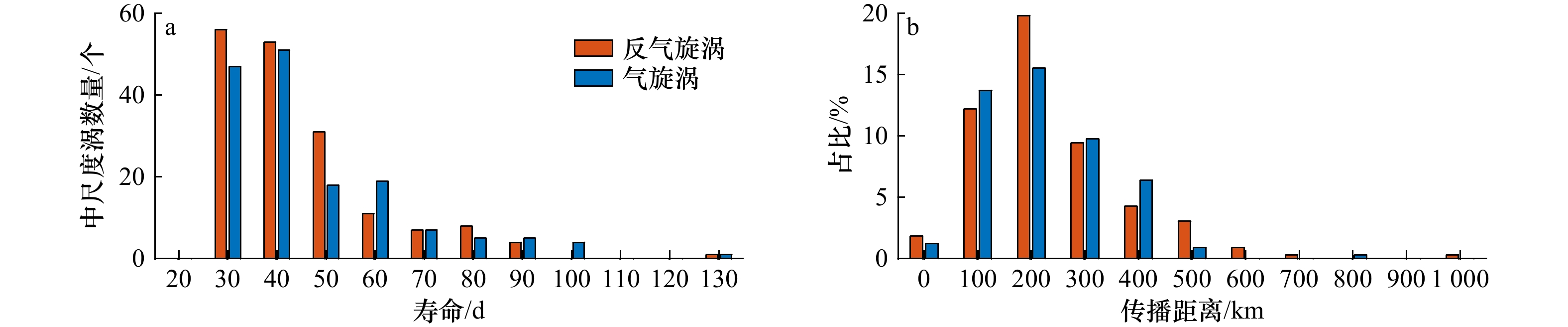
涡旋生成到消亡跨越时长定义为涡旋寿命。统计显示,安达曼海中尺度涡最短寿命为28 d,最长寿命为131 d,平均寿命约为46.4 d,其中反气旋涡平均寿命(45.5 d)短于气旋涡(47.4 d)。从分布来看(图3a),反气旋涡和气旋涡相似,均以小于65 d的短寿命涡旋为主,占总涡旋数量的87.05%,并且62.95%的涡旋寿命在25~45 d范围,超过百天的仅有4例 。相比于南海涡旋,安达曼海涡旋寿命较短,这可能与安达曼海宽度较窄有关。
涡旋生成地与消亡地之间的距离定义为传播距离,其概率分布如图3b所示。可见,安达曼海中尺度涡传播距离较短,涡旋传播距离不超过350 km的涡旋占绝大多数(约占全部涡旋的83.13%),反气旋涡与气旋涡分别占其总数的82.66%和83.65%,而传播距离超过550 km的涡旋数量仅有5个反气旋涡和1个气旋涡。反气旋涡的平均传播距离(241.1 km)大于气旋涡(221.5 km)。
3.2 涡旋动力特征
3.2.1 半径、振幅和旋转速度
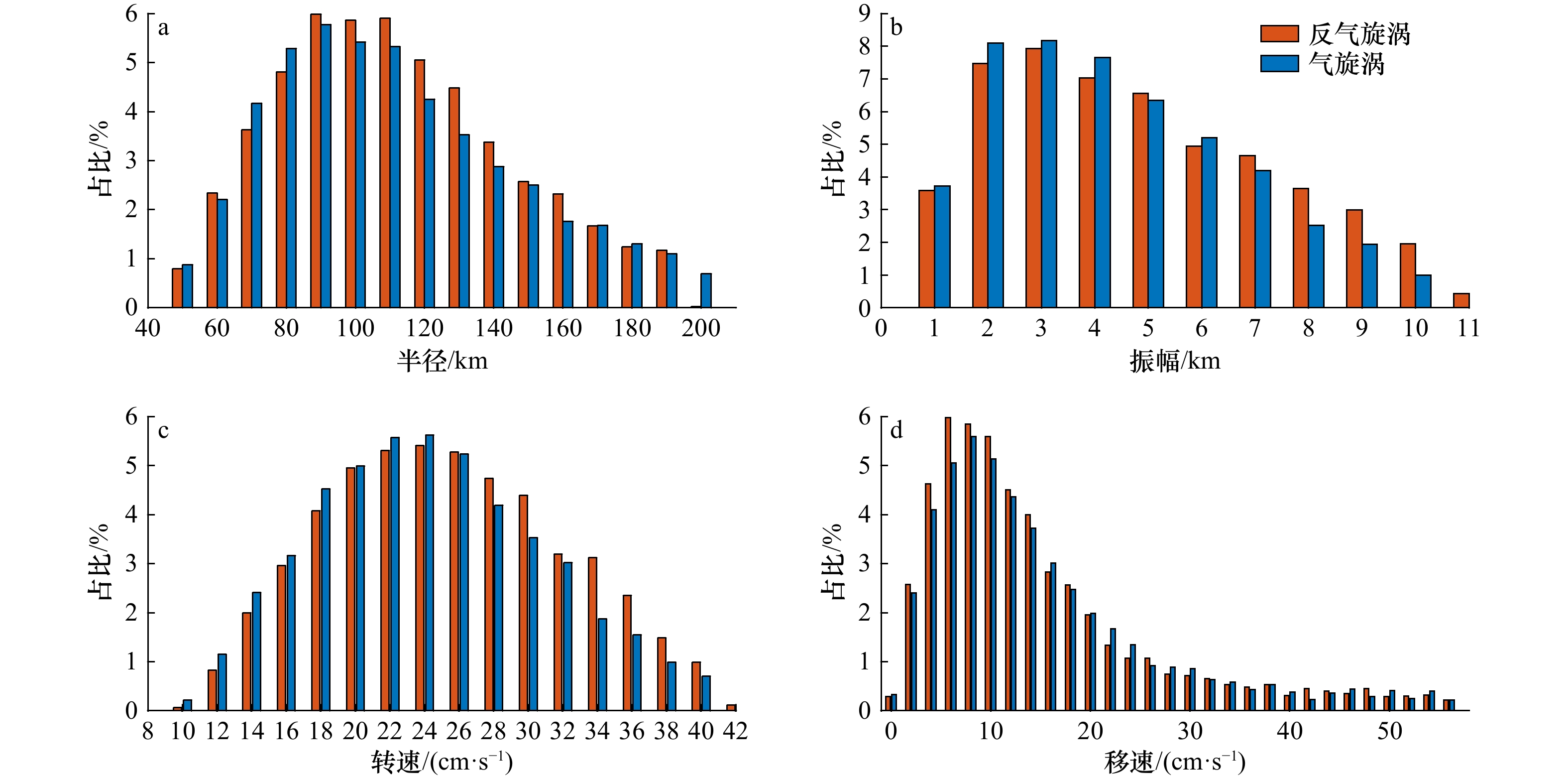
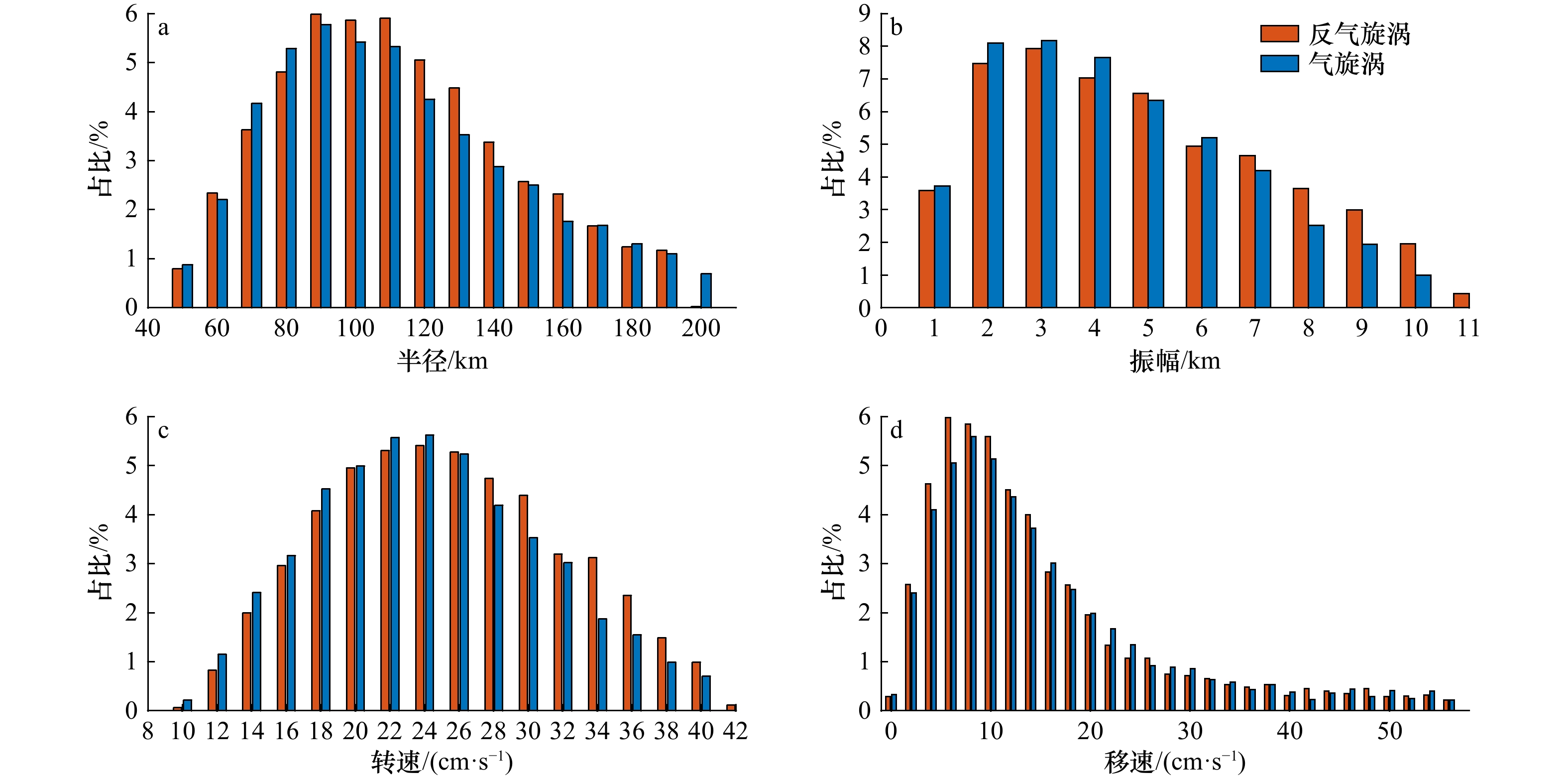
对安达曼27 a每天的涡旋特征进行统计,并剔除大于2倍标准差的异常值进行平均[14]。结果显示,全部每天涡旋的平均半径为(111.8 ± 34.2) km,反气旋涡的平均半径((112.2 ± 33.2) km)略大于气旋涡((111.4 ± 35.2) km);平均振幅为(4.7 ± 2.4) cm,其中反气旋涡振幅((4.9 ± 2.5) cm)高于气旋涡((4.5 ± 2.3) cm);平均最大旋转速度为(24.8 ± 6.7) cm/s,其中反气旋涡为(25.4 ± 6.8) cm/s,气旋涡为(24.2 ± 6.5) cm/s;平均移动速度为(15.0 ± 11.6) cm/s,其中反气旋涡的平均移动速度为(14.7 ± 11.5) cm/s,略慢于气旋涡的平均移动速度为(15.2 ± 11.6) cm/s。
图4显示出全部每天的涡旋半径、振幅、旋转速度和移动速度的概率分布直方图。由图4a可见,反气旋涡和气旋涡特征的半径分布规律在统计学上没有明显差异,75.74%的涡旋半径集中分布在65~145 km之间。涡旋半径基本为右偏的瑞利分布,这与Cheng等[21]统计北太平洋中尺度涡的结论一致。
图4b表明,反气旋涡和气旋涡振幅在2~3 cm处的分布概率最大。振幅小于7.5 cm的涡旋占全部涡旋数的85.53%,其中气旋涡比例更高为88.85%,反气旋涡略低为82.37%。振幅超过8.5 cm的强涡旋仅占全部涡旋的8.30%,其中反气旋涡为10.50%,气旋涡为6.01%。总体来看,反气旋涡和气旋涡振幅分布为右偏的瑞利分布,在3.0 cm左右占比分别高达7.93%和8.17%。
不同于半径和振幅分布,旋涡转速基本为正态分布特征(图4c),反气旋涡(气旋涡)在23~25 cm/s的分布概率最大达到5.41%(5.62%)。总体来看,在9~25 cm/s范围,气旋涡转速的分布概率高于反气旋涡,而在27~42 cm/s范围反气旋涡分布概率更高。
如图4d所示,涡旋移动速度的瑞利分布右偏更为明显,峰值分别对应于6 cm/s(AE)和8 cm/s(CE),但移速30 cm/s以上的比例超过10%。关注涡旋移速的主要分布范围,可见58.52%的涡旋集中分布在4~14 cm/s 范围内,反气旋涡和气旋涡分别约占其总数的59.93%和57.07%。该范围与纬度相近的南海南部海盆(6~12 cm/s)[22]结果较为一致。
3.2.2 移动轨迹和方向
对安达曼海涡旋纬向移动轨迹进行统计分析,结果如表1所示。可见,受β效应的制约[23-24],83.63%的反气旋涡(143个)和73.89%的气旋涡(116个)向西移动。反气旋涡平均向西移动1.72°,远于气旋涡的1.61°。这与涡旋移动距离的对比结果一致。相比反气旋涡,气旋涡生成位置更靠西,距离西边界安达曼群岛更近(图2),这可能是气旋涡移动距离近和所跨经度少的原因。
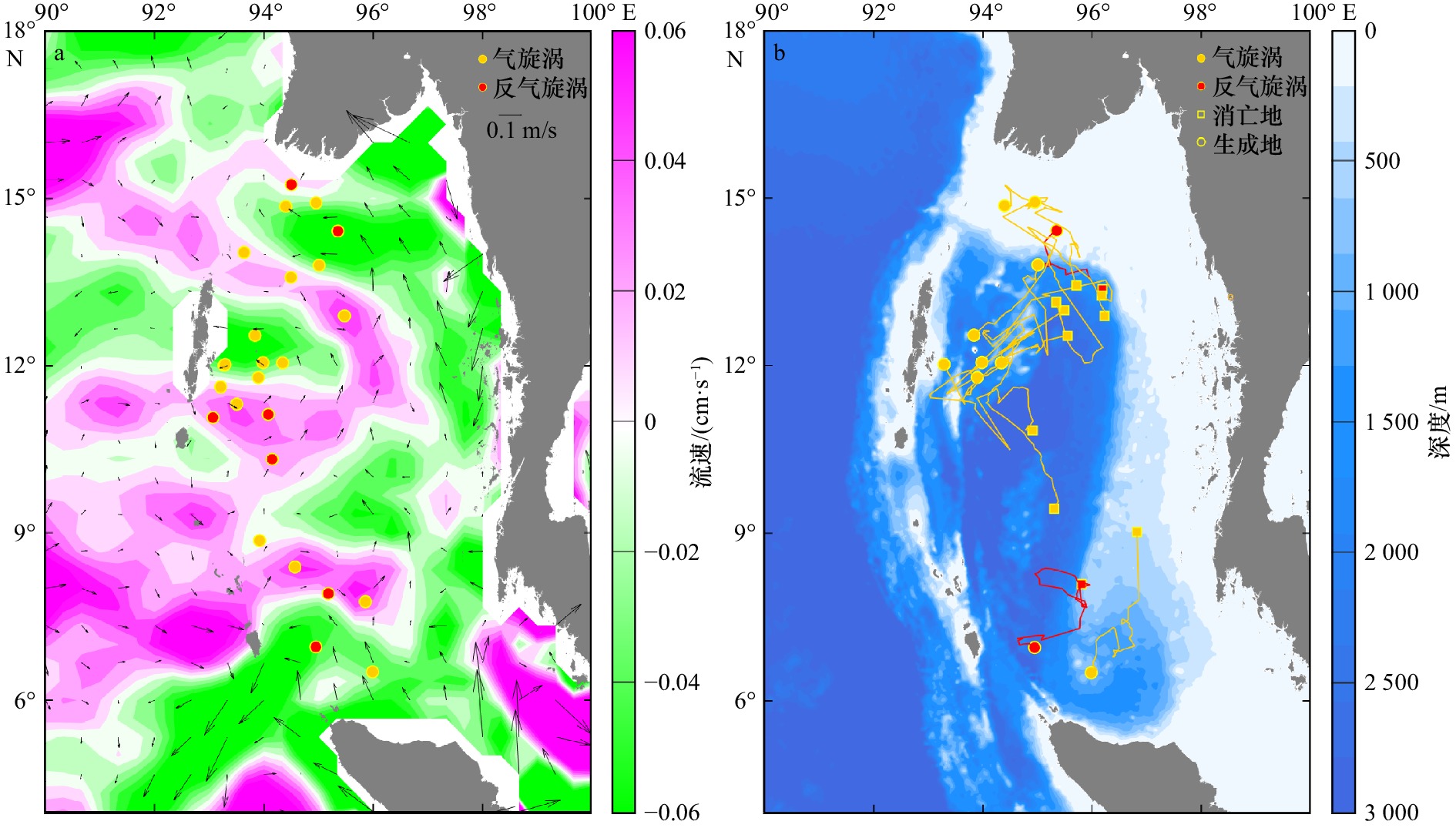
表 1 涡旋纬向运动特征统计Table 1. Statistical analysis of zonal motion characteristics传播方向 涡旋极性 数量 占比 平均移动经度 空间分布 西向传播 AE 143 83.63% 1.72° 整个安达曼海 CE 116 73.89% 1.61° 东向传播 AE 28 16.37% 0.63° 安达曼海东部海域 CE 41 26.11% 0.71° 安达曼海西部海域 除了西向移动涡旋,我们发现还有28个反气旋涡(占全部反气旋涡的16.37%)和41个气旋涡(占全部气旋涡的26.11%)向东移动,并且气旋涡东向移动距离(0.71°)远于反气旋涡(0.63°)。图5a显示出东移显著(东移距离大于0.7°)的涡旋生成地空间分布及其对应背景纬向流速。可见东移显著的24个涡旋主要分布在安达曼海西边界,54.17%的东移涡旋(反气旋涡5个,气旋涡8个)位于背景东向流速中,且气旋涡主要位于东向强流(大于0.04 m/s)。图5b显示出11个位于西向流中的东移显著涡旋的轨迹,以气旋涡为主,苏门答腊岛东北部和安达曼群岛东侧的涡旋主要沿着等深线向东北方向移动,而安达曼海北部的涡旋则沿等深线向东南方向移动。图5结果表明涡旋向东移动受背景纬向流的影响,同时还受到地形等因素影响。Peng等[25]认为相比于风,背景流对涡旋的传播方向影响更大,尤其是东向移动的涡旋对流速的变化比西向移动的涡旋更加敏感。另外,他们还发现涡旋有沿等深线传播的趋势。对于东向移动的涡旋来说,涡旋位置周围的地形越复杂,这种趋势就越明显。这与本文结果类似。
 图 5 显著东移涡旋的生成位置(点)及对应的背景纬向流(a)和在西向背景流中显著东移涡旋的移动轨迹(b)Figure 5. The generation location of significant eastward propagating eddies (dots) and corresponding background zonal flow (a) and the significant eastward propagation trajectories of the cyclonic (orange lines) and anticyclonic (red lines) eddies in the westward background flow (b)
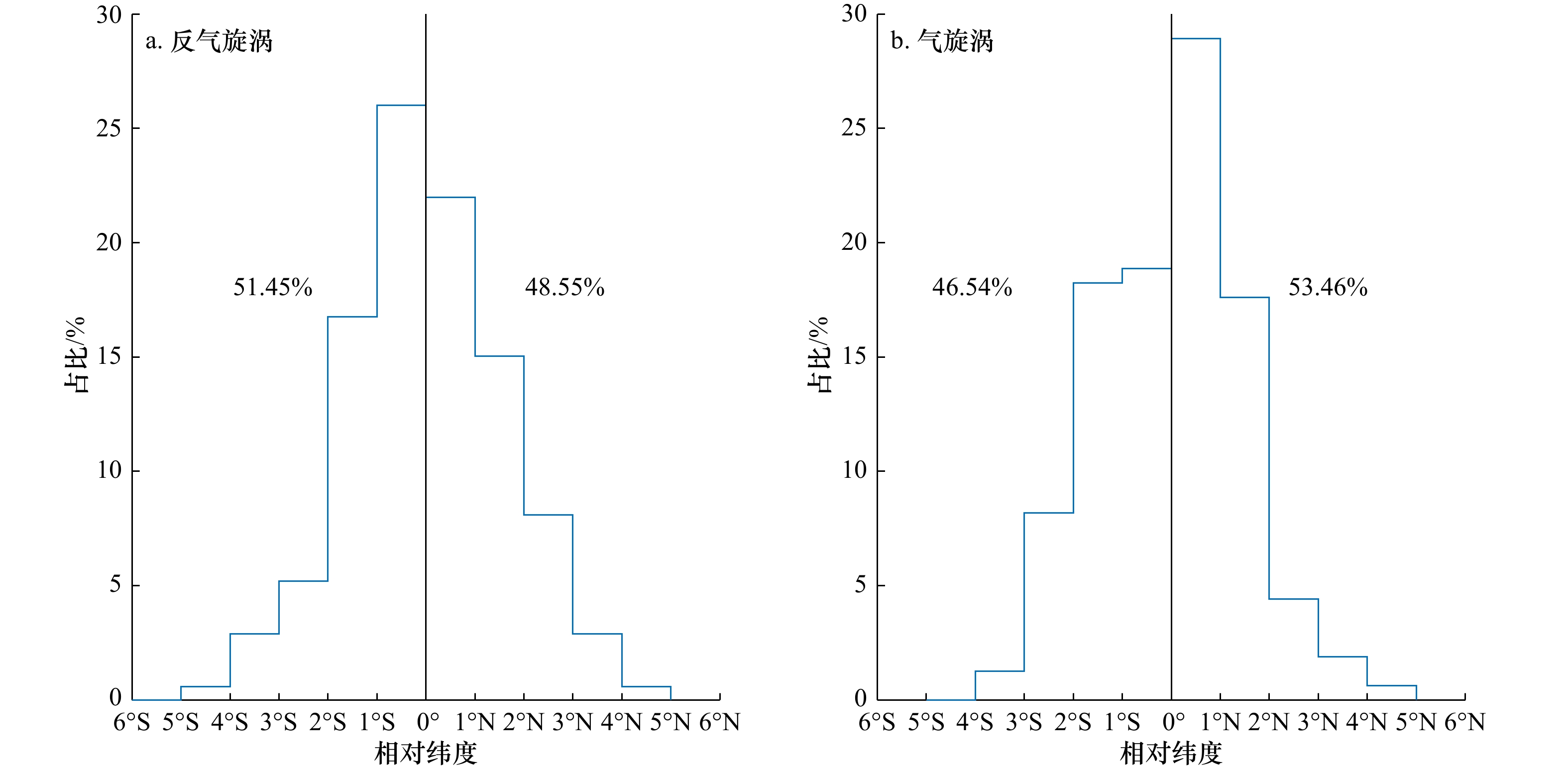
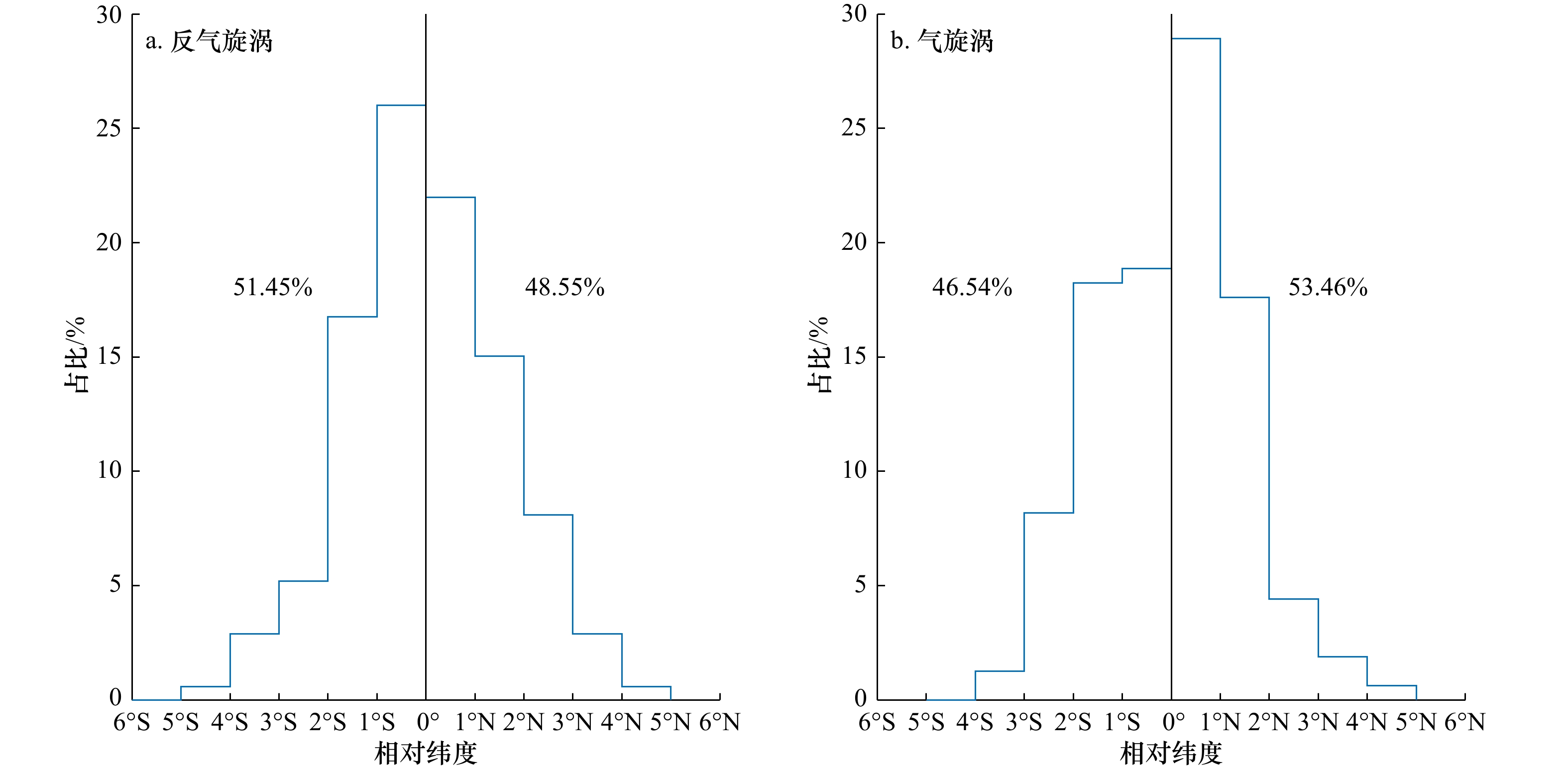
图 5 显著东移涡旋的生成位置(点)及对应的背景纬向流(a)和在西向背景流中显著东移涡旋的移动轨迹(b)Figure 5. The generation location of significant eastward propagating eddies (dots) and corresponding background zonal flow (a) and the significant eastward propagation trajectories of the cyclonic (orange lines) and anticyclonic (red lines) eddies in the westward background flow (b)除了纬向移动,反气旋涡和气旋涡移动轨迹也呈现经向分量。如图6所示,有48.55%的反气旋涡和53.46%的气旋涡向极地移动,有51.45%的反气旋涡和46.54%的气旋涡向赤道移动。这意味着反气旋涡运动有向赤道偏离的趋势,而气旋涡运动则有向极地偏离的趋势。这一结论与Chelton等[26]的研究结论相一致,然而安达曼海中尺度涡径向移动距离很短,47.89%的涡旋经向移动在1°内,可能与涡旋生命周期较短有关。
3.2.3 涡旋性质在生命周期上的演变
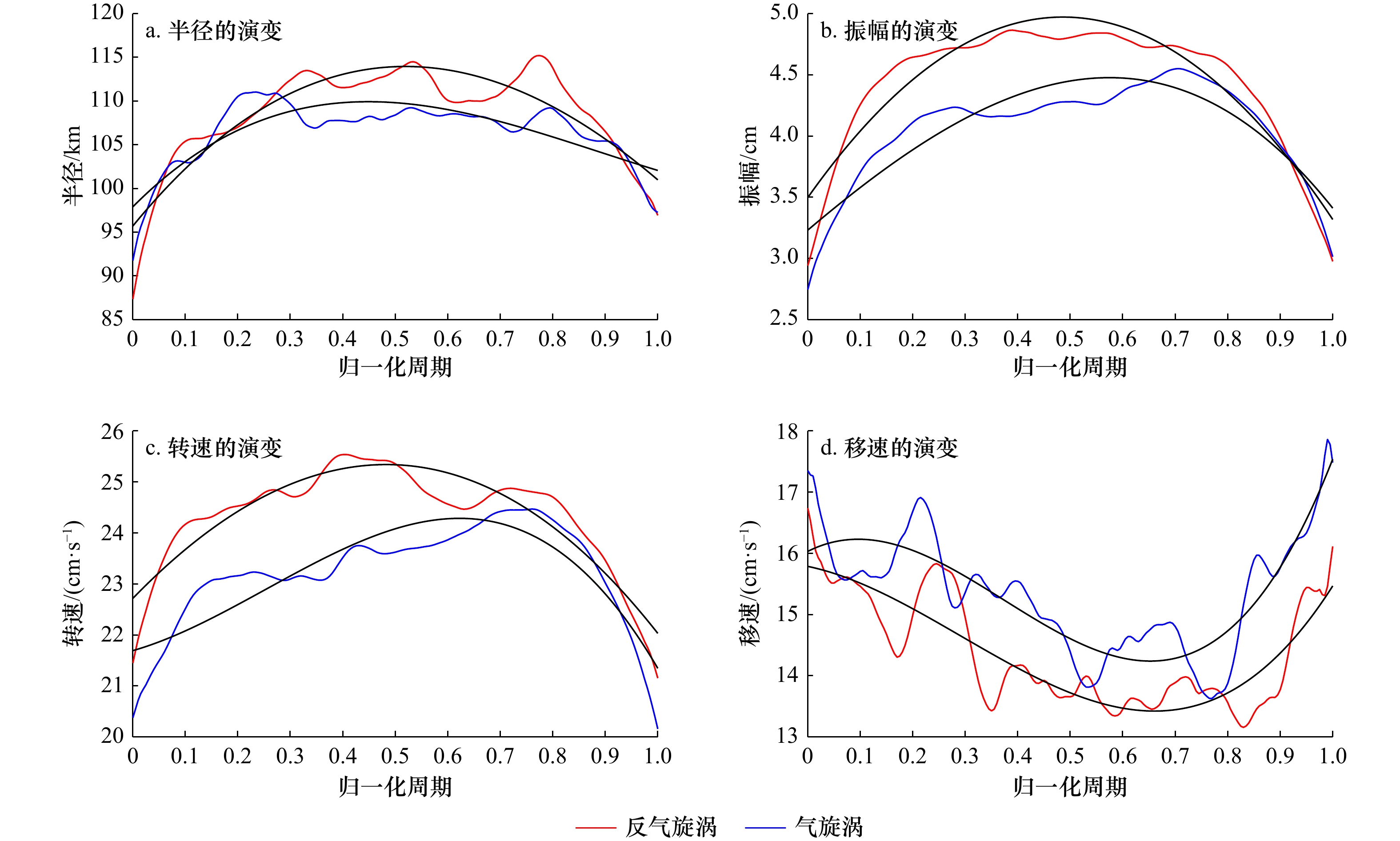
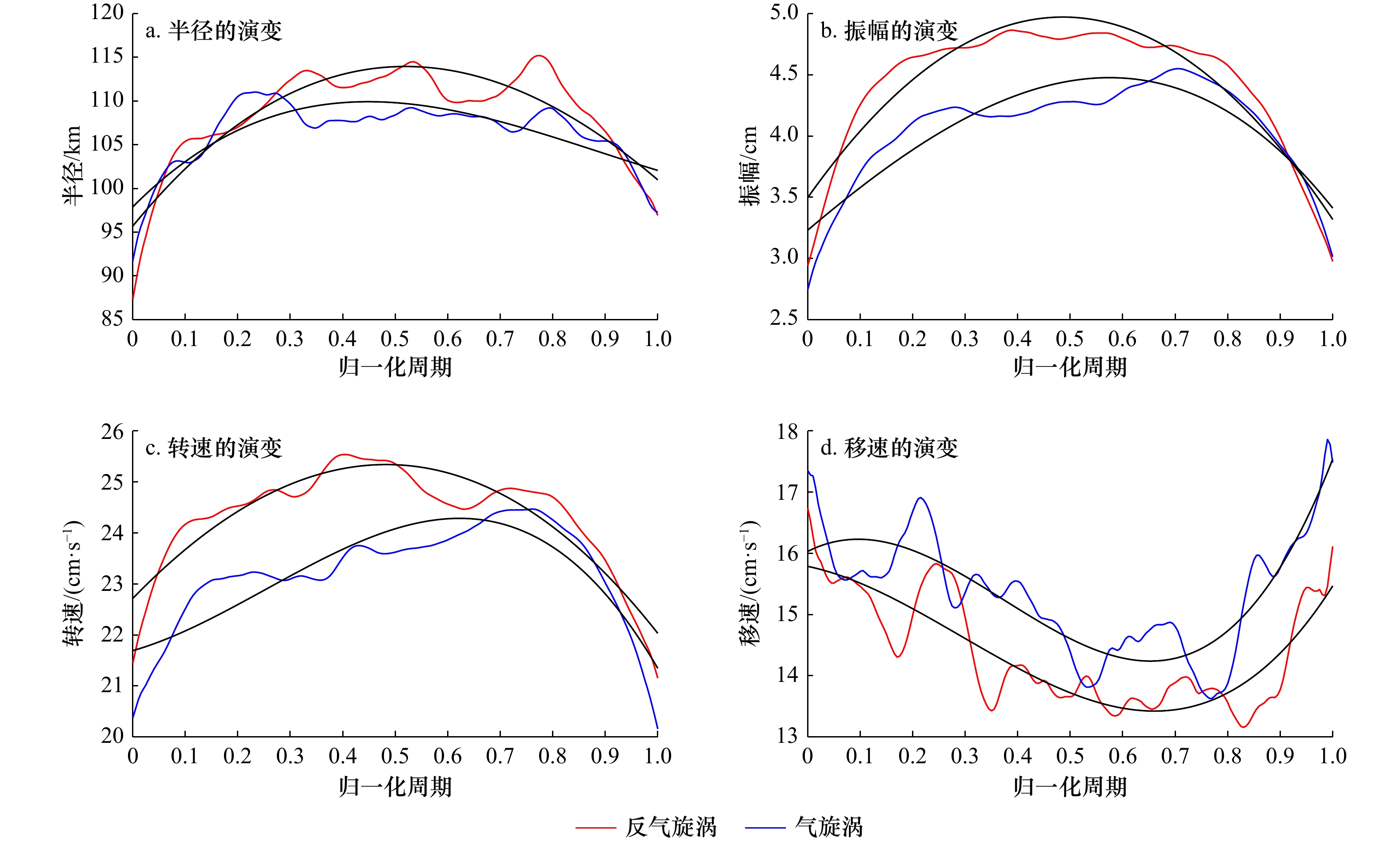
对涡旋生命周期进行归一化处理,进一步分析涡旋半径、振幅、转速和移速在其生命周期内的演变特征。由图7a可见,反气旋涡和气旋涡半径均呈现在生命初期增大、末期减小的特征。不同的是,反气旋涡在0.7~0.8周期时半径达最大值,而气旋涡在0.2~0.3周期时最大,并且在0~0.3生命初期气旋涡半径略大于反气旋涡,0.3~0.9周期时则相反。图7b和图7c所示的涡旋振幅和转速随涡旋生命周期演变显示出相似特征,0~0.3周期内二者均快速增大,之后缓慢增加,在0.7周期后迅速减小。在整个生命周期上,反气旋涡振幅和转速均大于气旋涡。
与半径、振幅和转速演变特征相反,涡旋移动速度在生命周期上呈现先减小、后增大的趋势(图7d),并且气旋涡移动速度整体上大于反气旋涡。这与Huang等[22]研究南海深海盆中尺度涡移速的生消演化得到的结果相似,涡旋移动速度与其寿命期间的旋转速度之间存在很强的负相关性,运动能量在生长阶段转换为旋转能量,而在耗散阶段则相反。在生长阶段,考虑到背景环流对传播速度的影响以及与正压和斜压不稳定性相关的涡旋产生机理,从大尺度背景流场到中尺度涡旋可能存在能量正级串和涡旋能量与大尺度环流相互转化,从而降低了移动速度并提高了旋转速度。
4. 涡旋季节变化
4.1 涡旋特征季节变化——跷跷板现象
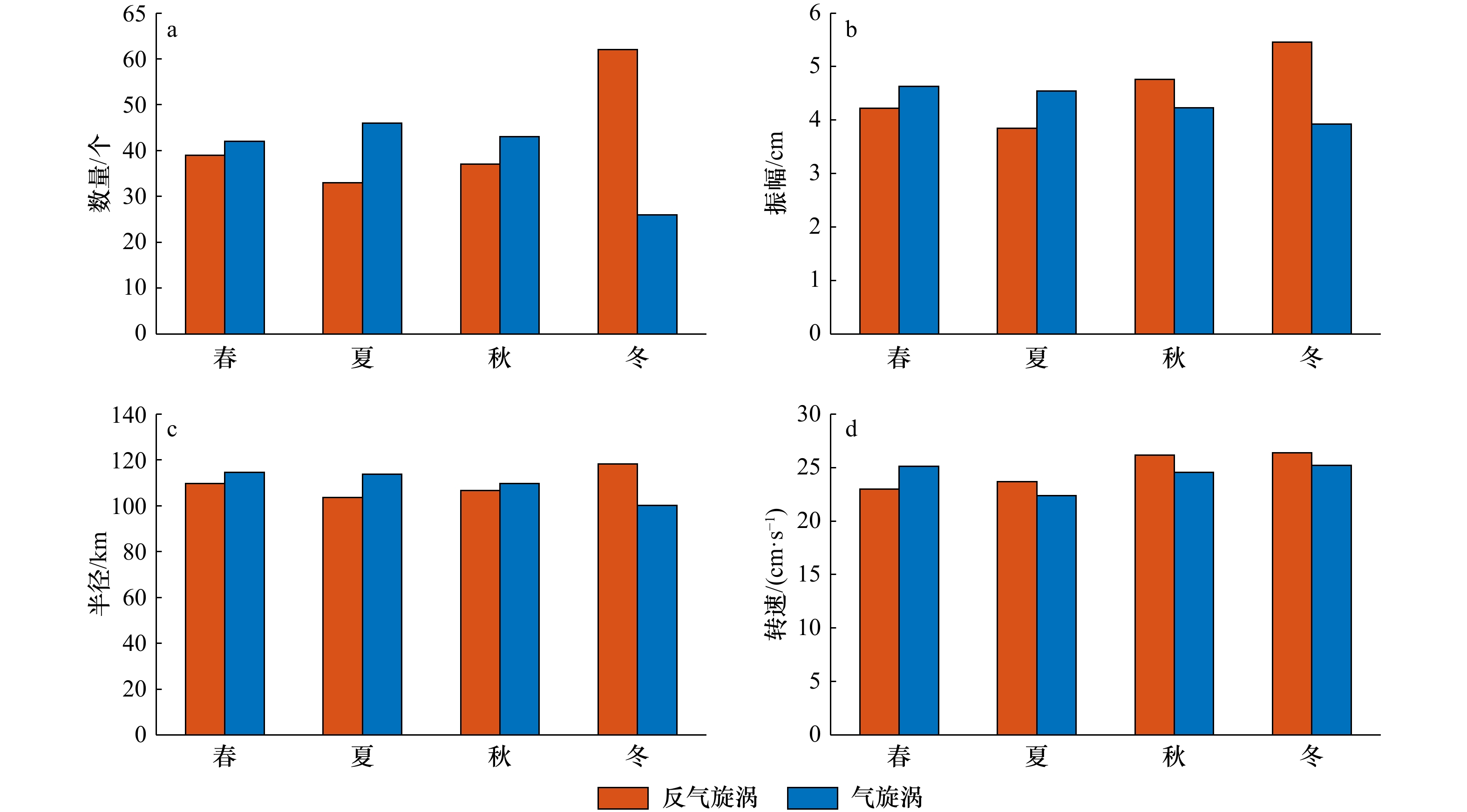
对涡旋数量、振幅、半径、转速等特征进行季节分析,结果如图8所示。图8为安达曼海涡旋特征的季节分布。就涡旋生成数量而言(图8a),春冬季涡旋数量多,夏秋季涡旋数量少,其中冬季最多,达到88个,春季次之,夏季最少,仅有79个。春秋季的反气旋涡和气旋涡个数大体相当,夏冬季反气旋涡和气旋涡的数量出现“跷跷板”变化,即夏季气旋涡居多,而冬季反气旋涡个数多于气旋涡的两倍。这与Cui等[15]统计得到的孟加拉湾结果有所不同,说明安达曼海与毗邻的孟加拉湾,虽同受季风影响,但仍受局地过程影响。对图8b至图8d对比分析可得,反气旋涡特征具有明显的季节变化特征,所有参量均夏季最小,冬季最大;气旋涡振幅和半径冬季最小,春季最大,而转速变化趋势与反气旋涡一致,夏季最小,冬季最大。反气旋涡和气旋涡的振幅和半径的相对大小在冬夏两季也出现跷跷板变化,即夏天气旋涡比反气旋涡更强更大,冬季则反气旋涡更强更大。
4.2 涡旋分布特征季节变化——极性反转现象
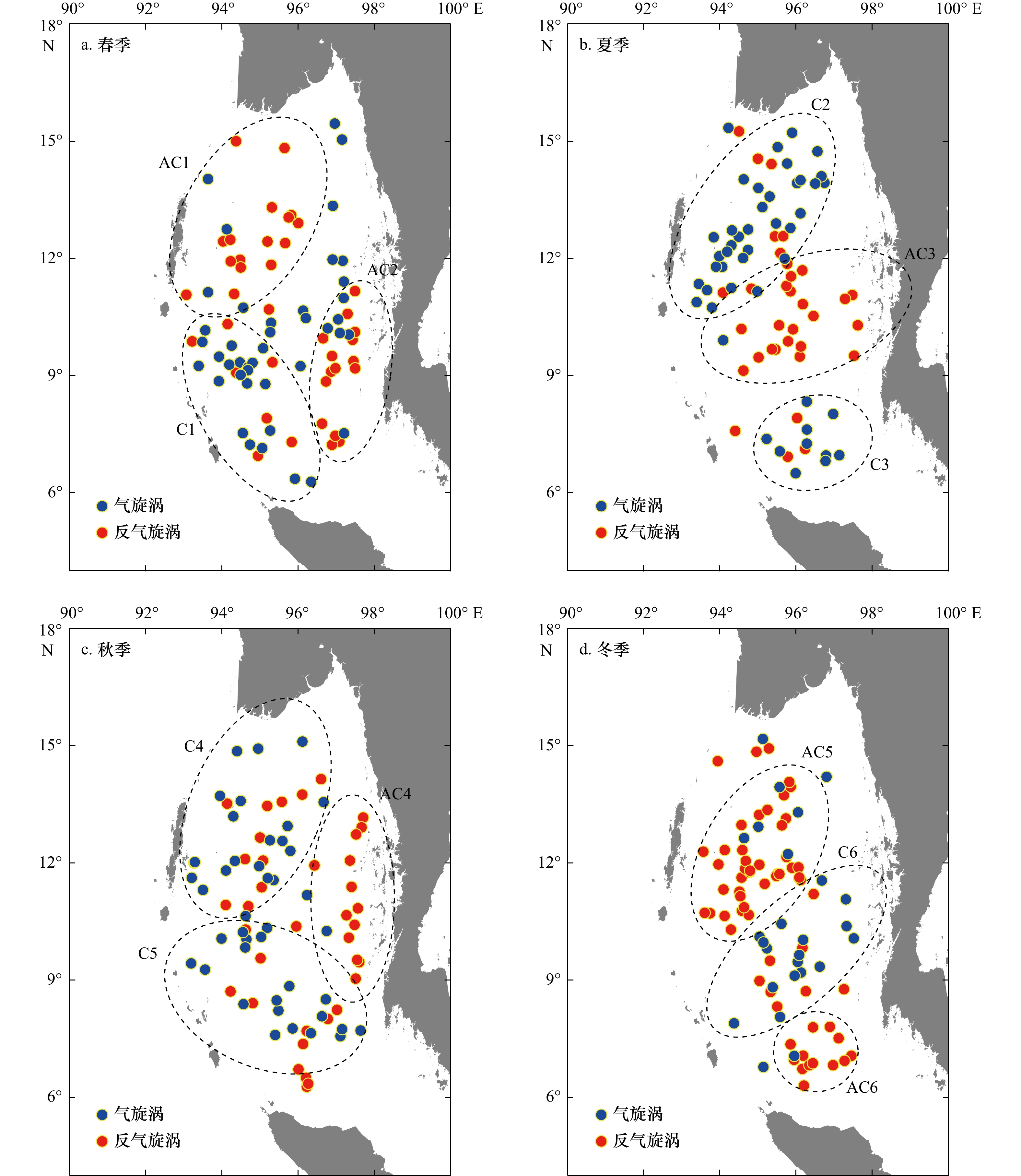
图9示出安达曼海中尺度涡生成位置季节变化的空间分布。可见,安达曼海中尺度旋涡的空间分布存在明显的同极性涡旋聚集特点。为此根据涡旋极性,划分不同的涡旋聚集区,反气旋涡聚集区命名为AC1−AC6,气旋涡聚集区命名为C1−C6。
如图9a所示,春季安达曼海涡旋分布呈现“西北−西南−东”聚集特征。西北是一个反气旋聚集发生区AC1,西南侧存在一个气旋聚集发生区C1,东侧(马来半岛附近)存在一个反气旋聚集发生区AC2。春季反气旋涡和气旋涡总体数量大体相当(数量比为39∶42),不同聚集区差别明显。北侧AC1反气旋涡有16个,东侧AC2反气旋涡有15个,南侧C1有19个气旋涡,另有部分气旋涡散落海盆东北侧。
夏季(图9b)涡旋总数量最少,为79个,空间聚集呈“北−中−南”特征。相比春季,夏季涡旋更集中到海盆中央,反气旋涡数量较少,气旋涡数量在总体上占优势。涡旋分布从北向南呈“气旋−反气旋−气旋”的交替分布,北部是气旋涡聚集区C2,中部是反气旋涡聚集区AC3,南部是气旋涡聚集区C3。从涡旋数量上来看,北部C2 最多,有34个气旋涡,中部AC2 有22个反气旋涡,南部C3 最少,只有10个气旋涡,从北往南涡旋聚集区涡旋数量比近似为3∶2∶1。
秋季(图9c)中尺度涡数量和空间分布与春季类似的特征,但各聚集区位置和方向较春季偏北偏西,并且“西北”聚集区由春季的AC1转为气旋涡偏多的C4,东侧反气旋涡聚集区AC4呈现明显的南北向分布。从涡旋数量上来看,西北C4有21个气旋涡,西南C5有14个气旋涡,东部AC4存在13个反气旋涡。
冬季(图9d)中尺度涡也主要集中分布在安达曼海中央深水区,空间聚集呈“北−中−南”特征,但涡旋极性与夏季相反。从北向南呈“反气旋−气旋−反气旋”的交替分布,北部是反气旋涡聚集区AC5,中部是气旋涡聚集区C6,南部是反气旋涡聚集区AC3。从总数量上看,反气旋涡(62个)比气旋涡个数(26个)占统治性优势。对于不同极性涡旋的聚集区,北部AC5最多,有35个反气旋涡,中部C6和南部AC6分别存在17个气旋涡和13个反气旋,从北往南涡旋聚集区涡旋数量比近似为3∶1∶1。
综上所述,夏冬两季安达曼海中尺度涡位置分布具有典型的极性反转的交替分布特征,夏季从北向南呈“气旋−反气旋−气旋”的交替分布,而冬季则与之相反为“反气旋−气旋−反气旋”。春秋两季涡旋位置分布相对不规则,具有过渡特征。
4.3 涡旋分布季节特征调控机制
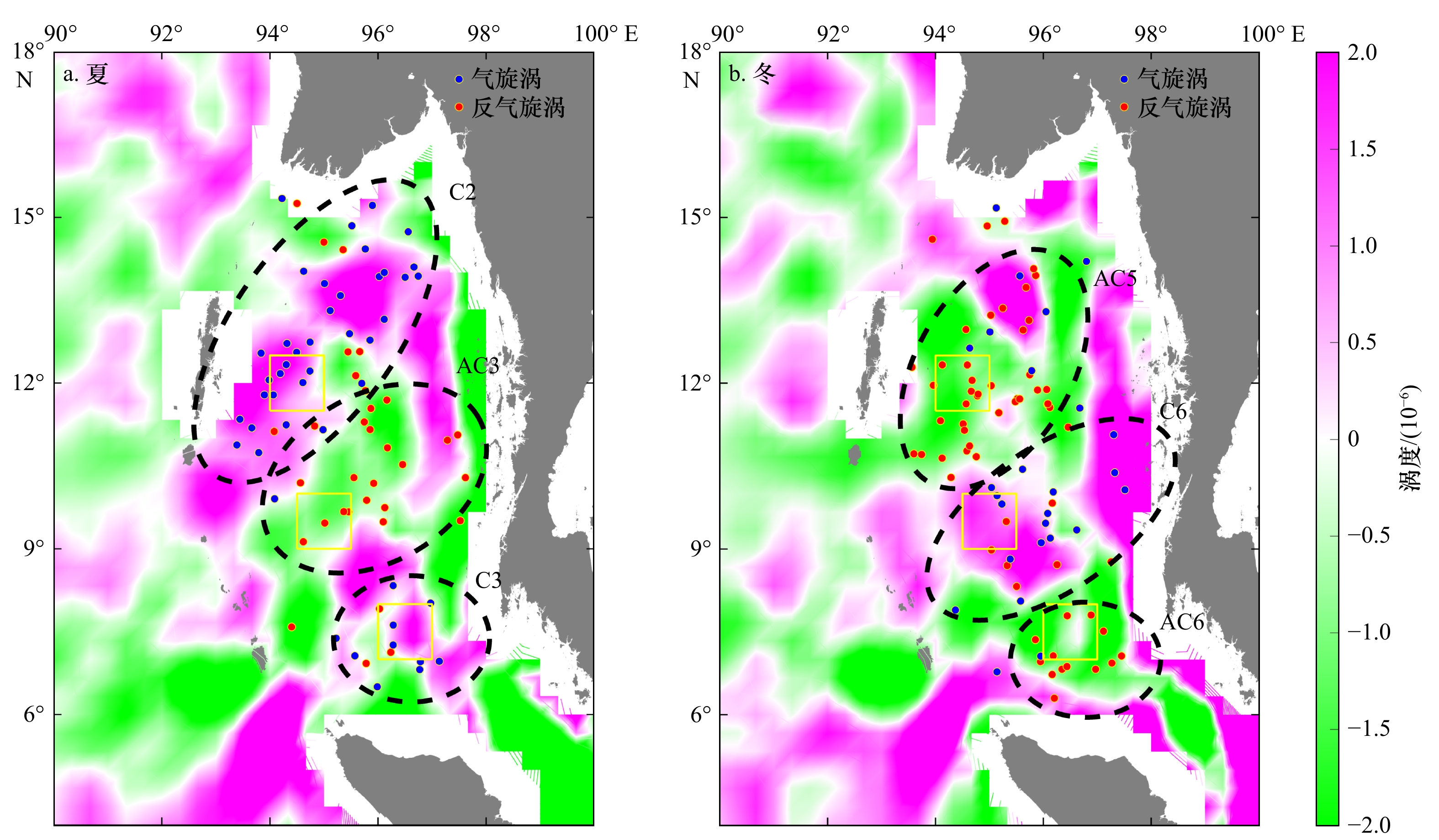
在上一节研究中可知,安达曼海中尺度涡存在明显的季节变化。Chen等[13]分析班达海中尺度涡分布季节性反转提出背景涡度场对涡旋极性变化具有重要作用。本节将选取安达曼海夏、冬季节的海面流场涡度进行分析,探究其对安达曼海涡旋季节变化的影响。
图10显示出安达曼海气候态夏、冬季海面流场的涡度分布。可见,安达曼海海面流场涡度具有正负涡度交替分布特征,且存在同一位置的冬夏反转。夏季(图10a),流场涡度从北向南呈“正−负−正”的交替分布,北部气旋涡聚集C2区以正涡度为主(紫色)、中部反气旋涡聚集AC3区则以负涡度为主(绿色)、南部气旋涡聚集的C3区则又以正涡度为主(紫色)。冬季(图10b),流场涡度分布则与夏季相反,从北向南呈“负−正−负”的交替分布。
 图 10 安达曼海夏(a)、冬(b)两季海面流场涡度(彩色)及涡旋生成位置(点)实心红点为反气旋涡,实心蓝点为气旋涡。缩写C2 和AC3等指气旋或反气旋聚集发生区Figure 10. Background circulation vorticity (color) and eddy generating locations (dots) of Andaman Sea in summer (a) and winter (b)Red and blue dots represent anticyclonic and cyclonic eddies, respectively. Abbreviations (i.e., C2, AC3) mark the cluster regions of cyclonic or anticyclonic eddies
图 10 安达曼海夏(a)、冬(b)两季海面流场涡度(彩色)及涡旋生成位置(点)实心红点为反气旋涡,实心蓝点为气旋涡。缩写C2 和AC3等指气旋或反气旋聚集发生区Figure 10. Background circulation vorticity (color) and eddy generating locations (dots) of Andaman Sea in summer (a) and winter (b)Red and blue dots represent anticyclonic and cyclonic eddies, respectively. Abbreviations (i.e., C2, AC3) mark the cluster regions of cyclonic or anticyclonic eddies理论上,Shi等[27]基于非线性位涡方程,给出纬向流中孤立罗斯贝波(涡)宽度
$ \mathrm{\omega } $ (正实数)与孤立波(即涡旋)振幅A0和背景流剪切δ乘积的平方根成反比,即$$ \omega \approx \frac{3\mathrm{m}\left|\mathrm{\beta }+{F}u_{0}\right|}{\left({{n}}^{2}{\text{π}}^{2}+{F}\right)\sqrt{\mathrm{\varepsilon }}}\frac{1}{\sqrt{\left[1-{\left(-1\right)}^{{n}}\right]{n}{\text{π}}}\sqrt{{{A}}_{0}\mathrm{\delta }}},$$ (4) 式中,m为雅克比椭圆函数的模;n为罗斯贝波模态数;u0为背景纬向流;δ为流的剪切;A0为孤立波(即涡旋)的振幅。这意味着,涡旋的极性即振幅A0的正负与背景流的涡度−δ(纬向流的南北向剪切等于负涡度)同符号[13]。尽管该理论为纬向流中的结果,在坐标转换下,以背景流方向为纬向,该结论仍可适用,即背景流正涡度(δ < 0)对应涡旋振幅A0< 0,涡旋为冷涡,反之为暖涡。
如图10a所示,夏季气旋涡聚集的海盆北部C2区和南部C3区,背景流涡度恰为正涡度,而海盆中部背景流为负涡度,则与暖涡聚集区AC3对应。在冬季(图10b),背景流涡度逆转时,涡旋极性也随之逆转。春秋两季涡旋极性与背景流涡度总体上也符合上述关系(图略)。相比冬夏两季,春秋季处于转换期,涡旋位置和背景场涡度分布相对散乱。这与过渡期背景场较为不稳定和复杂有关。因此可见,背景流场涡度可能是影响涡旋极性交替分布的重要机制。
4.4 涡旋生成与能量季节变化机制
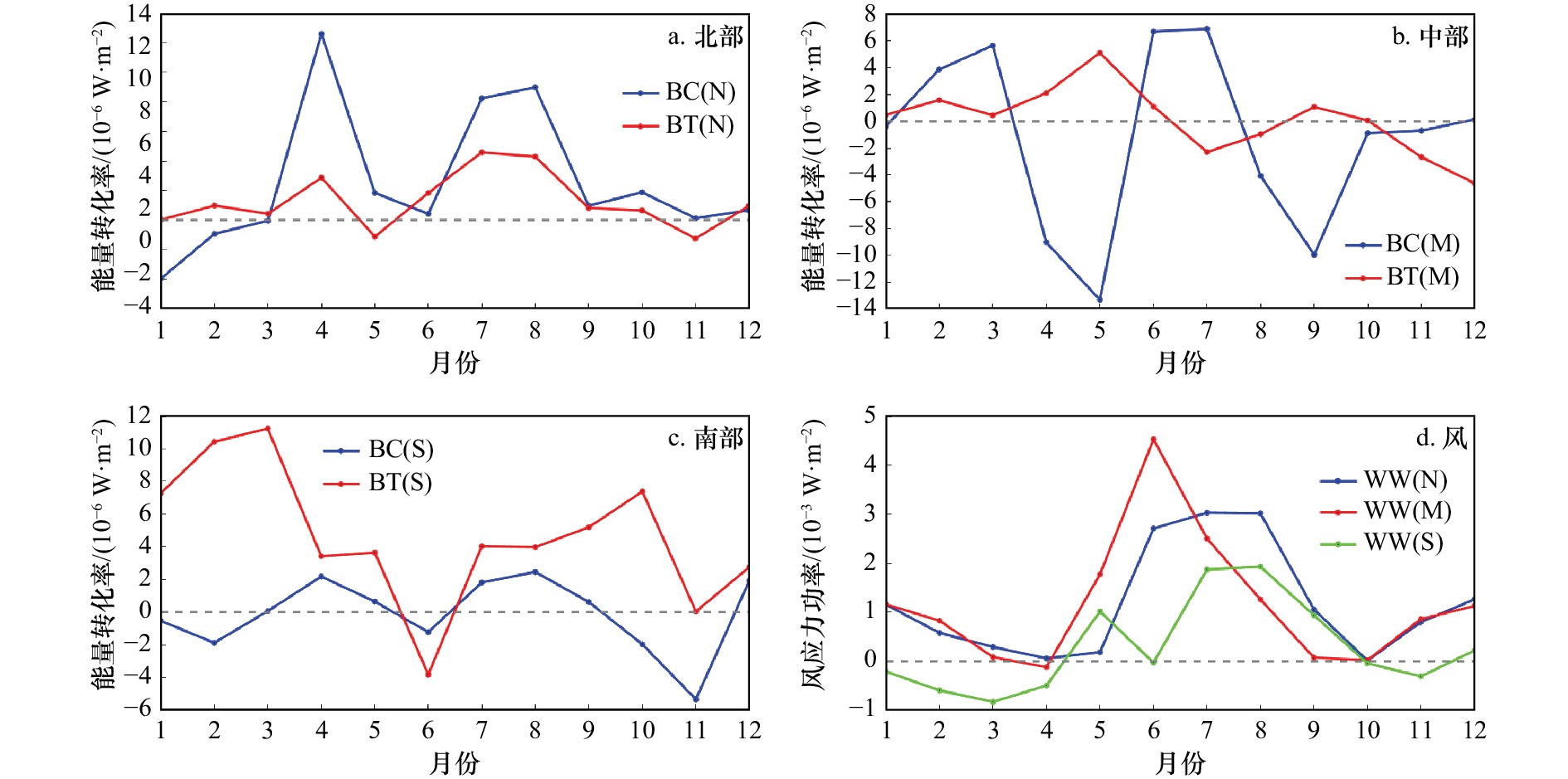
为了明确安达曼海中尺度涡的主要能量来源,选取夏冬季节涡旋聚集区中心位置代表安达曼海海盆北部(11.5°~12.5°N,94°~95°E)、中部(9°~10°N,94.5°~95.5°E)和南部(7°~8°N,96°~97°E),计算上层300 m(Lin等[28]认为涡旋在孟加拉湾引起的海洋异常主要局限于300 m以上深度)积分的斜压能量转化率(Baroclinic Eddy Energy Conversion Rate, BC)、正压能量转化率(Barotropic Eddy Energy Conversion Rate, BT)和风应力功率(Rate of Wind Stress Work, WW)[29]:
$$ {\rm{BC}}=-\int \frac{{g}^{2}}{{\rho }_{0}{N}^{2}}v'{\rho }'\cdot \nabla h\bar{\rho }{\rm{d}}z, $$ (5) $$ {\rm{BT}}=-\int {\rho }_{0}\frac{\partial \bar{{u}_{i}}}{\partial {x}_{i}}{u}_{i}'{u}_{j}'{\rm{d}}z, $$ (6) $${\rm{WW}}={\tau }_{w}{v}'_{0}, $$ (7) 式中,撇号表示相对气候态的异常值,上横线表示空间平均值;g是重力;N是浮力频率;
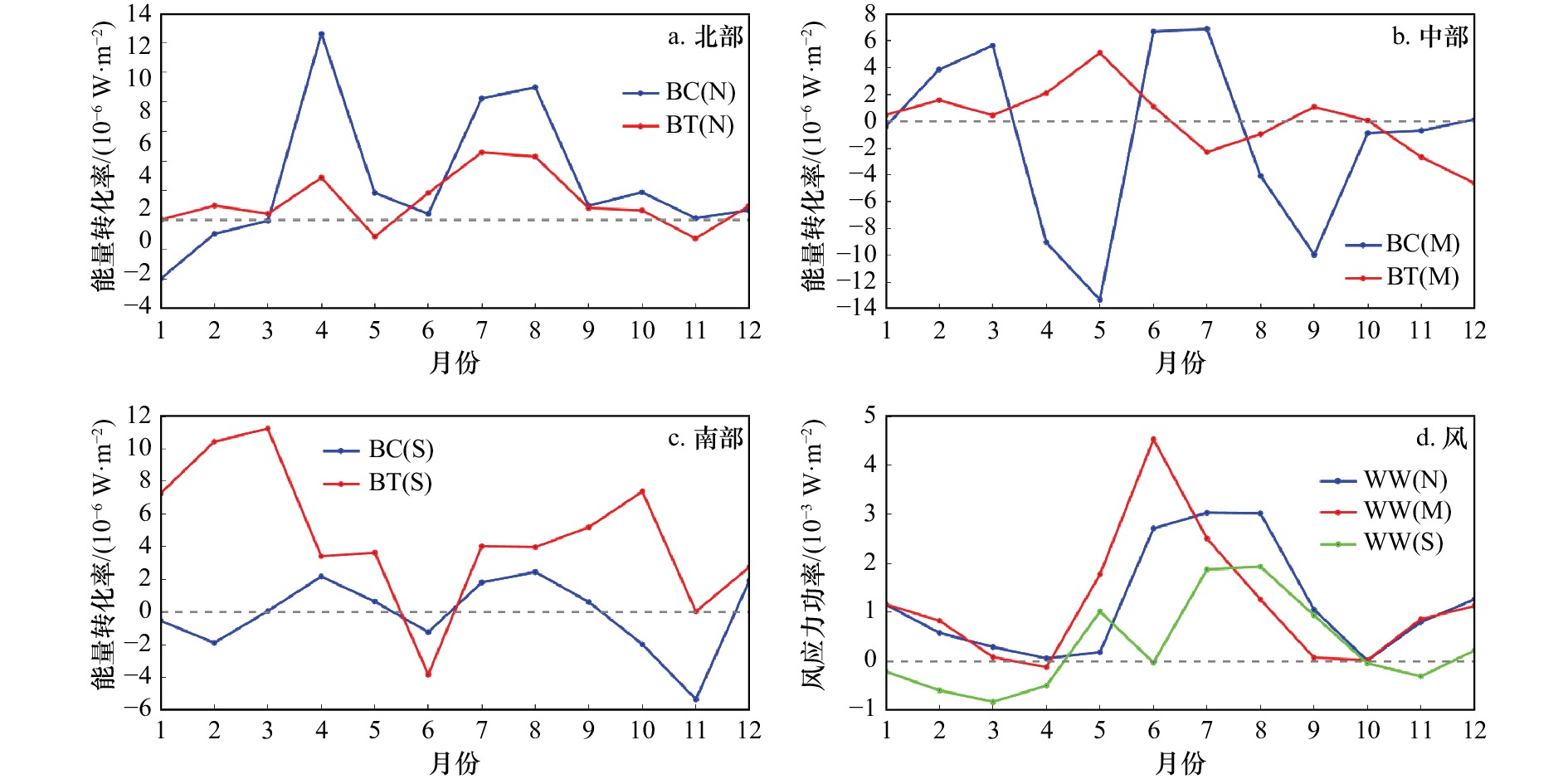
$ \nabla h $ 表示水平梯度;τw和v0分别表示风应力和海表面流速;ρ0是平均海水密度(ρ0= 1030 kg/m3),$\ \bar \rho $ 为气候态平均密度;下标i和j分别代表x和y方向重复索引求和。从物理意义上讲,正BC(BT)意味着平均势能(动能)转换为涡势能(动能),是产生斜压(正压)不稳定的原因。BC、BT和WW的月分布结果如图11所示,其中BT值已放大10倍。可见,WW在10−3 W/m2量级,远大于BC和BT的量级,说明风强迫是安达曼海中尺度涡能量变化的主要机制。具体到海盆北部(图11a),BT远小于BC,斜压不稳定大于正压不稳定。BC和BT以正值为主,二者均呈现4月和7−8月为高值的同步变化特征,冬季月份BC为负值,将减弱EKE。在海盆中部(图11b),斜压不稳定仍然大于正压不稳定,BC和BT变化呈现反位相,其中BC在冬夏为正值,春秋为负值,季节变化剧烈。在海盆南部(图11c),BT值增大,几乎与BC相当,二者基本同位相变化,在春秋出现高值,冬夏则为负值。海盆内WW变化趋势基本相同(图11d),即夏季WW最大,冬季次之,春秋季风转换期WW最小。除了海盆南部春冬季节,WW出现负值,其他均为风场向涡旋场输入能量。最大风强迫出现月份从海盆中部的6月推移到北部的8月。
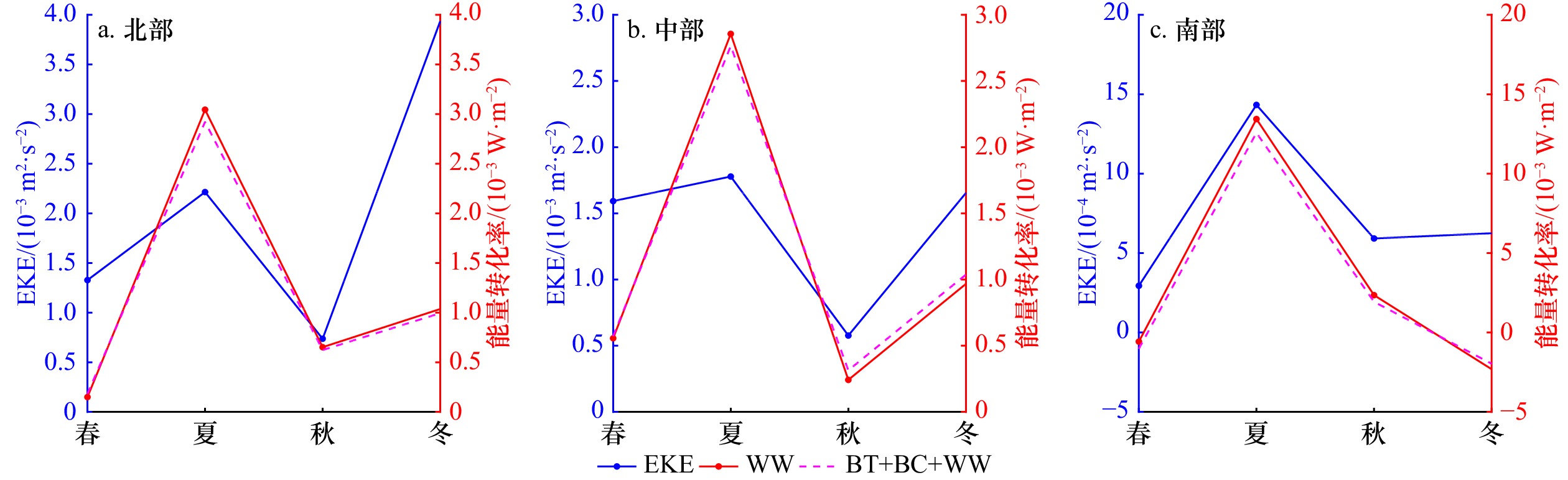
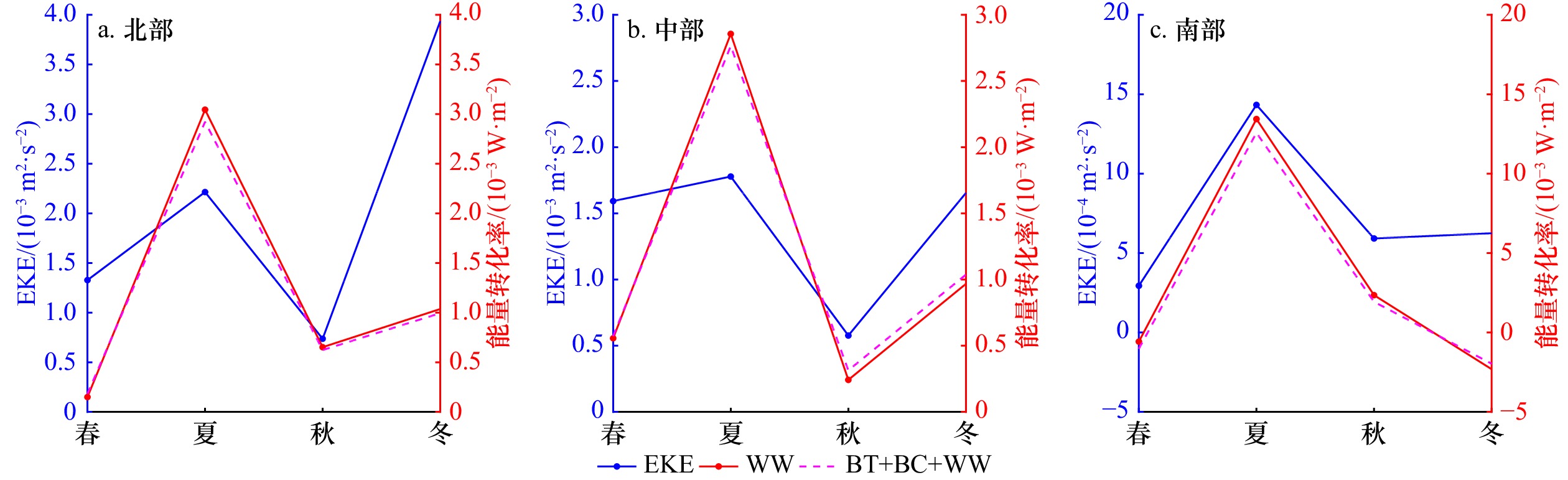
图12显示了安达曼海北部、中部、南部空间平均EKE、WW和能量输入总和(BC+BT+WW)的季节分布。可见,海盆从北向南均呈现EKE春秋低、夏冬高的特征。从能量输入来看,风应力做功与能量输入总和量级大小相同、季节变化趋势一致,夏季能量输入最高,而春秋季能量输入较少,这与夏季EKE高、春秋EKE低的特征吻合,说明风强迫是影响涡旋强弱的重要机制。
相比夏季,冬季能量总输入值较低,然而冬季EKE值约是夏季的两倍,这说明冬季除了BT、BC和WW外,还有其他能量来源。
Chen等[30]研究显示,除了海洋内部不稳定性,季节内振荡 (ISOs) 的大气强迫也对安达曼海区域的EKE起着重要作用。ISOs主要通过风应力产生EKE,包括赤道风的远程强迫和季风的局地强迫。有研究[31-32]认为,赤道风场激发的海洋波动传至印度洋东边界后以沿岸开尔文波的形式沿着苏门答腊−爪哇群岛向北传播,而后通过格雷特海峡进入安达曼海,在东边界激发出罗斯贝长波进而可对整个海盆流场进行调整。黄挺等[17]认为进入安达曼海的开尔文波可能通过两种机制诱发中尺度涡,一种是通过波峰(或者波谷)处的涡度异常脱落产生涡旋[33],还有一种是和安达曼海内的固有频率通过共振机制或者其他相互作用产生[34]。可见,除了局地强迫和不稳定,安达曼海中尺度涡还可能受到遥相关过程影响。遥强迫可能是冬季高EKE的产生源。
5. 讨论
5.1 安达曼海涡旋特征与其他海域对比
基于卫星高度计资料和多种涡旋探测、追踪方法,前人对全球[35]、各大洋开阔海域[36-37]、黑潮延伸体[38]、副热带逆流区[39]等涡旋活跃区域进行了大量中尺度涡统计分析。在南海、苏禄海、苏拉威西海、班达海等太平洋边缘海区的中尺度涡也进行了大量研究[13, 20, 41-42]。安达曼海地理位置特殊,中尺度涡演变规律对该海域航行等水上水下活动具有重要应用价值。同时,安达曼海作为小面积的边缘海,狭长海盆约束下中尺度涡特征有何不同,对认识海盆固有和中尺度涡群体特征具有科学意义 [34]。
表2显示出全球及安达曼海周边海域中尺度涡特征。可见,与平均寿命84.9 d、振幅7.7 cm的全球涡旋相比[35],安达曼海涡旋的寿命和振幅明显偏小,仅有全球平均的50%左右(约46.4 d和4.7 cm),但其半径(111.8 km)却比全球涡旋的平均值(82.4 km)大35.68%。由于安达曼海海盆较窄,其涡旋的平均传播距离(231.3 km)比全球涡旋的平均值(271.7 km)小14.87%;与全球平均类似,反气旋涡平均传播距离大于气旋涡。相比于孟加拉湾[15],安达曼海涡旋的平均寿命、振幅、半径和传播距离均偏低,分别为孟加拉湾涡旋平均值的84.36%、51.08%、90.16%和68.84%。对比南海、班达海和苏禄海等边缘海的涡旋平均特征,可以看出,随着海盆尺度的减小,涡旋半径和寿命的平均值也逐渐减小,海盆狭小的苏禄海的涡旋平均寿命和半径仅为海盆宽阔的南海涡旋平均值的1/2,证实了海盆固有模态对海盆内涡旋特征的约束[34]。Hao等[41]和Zhan等[42]在印度尼西亚海域和红海也都观察到了这种现象。受有限海盆空间尺度制约,狭窄且水深较浅的海峡阻碍了安达曼海涡旋的发展。需要注意的是,表2中南海涡旋仅统计了大于150 d的长寿命涡旋,孟加拉湾涡旋则是大于30 d的全部涡旋,涡旋传播距离与涡旋寿命成正比[43]。
表 2 全球及安达曼海周边海域中尺度涡特征Table 2. Mesoscale eddy characteristics of the world and the waters surrounding the Andaman Sea海域 海域长宽(南北/东西)/km 生命周期/d 涡旋振幅/cm 涡旋半径/km 传播距离/km 不同极性数量比/AE∶CE 全球[35] >10000 84.9
AE > CE7.7
AE < CE82.4
AE > CE271.7
AE > CE173245∶179127
AE < CE孟加拉湾[15] 2750/1600 55
AE < CE9.2
AE < CE124
AE > CE336
AE < CE389∶565
AE < CE南海[20] 2000/1000 61.6 \ 132 582.5 434∶393
AE > CE班达海[13] 450/1000 40
AE < CE4.1
AE < CE116
AE=CE165.3
AE > CE71∶76
AE < CE苏禄海[40] 790/600 32 1.88 76.6 \ 225∶243
AE < CE安达曼海 1100/600 46.4
AE < CE4.7
AE > CE111.8
AE > CE231.3
AE > CE171∶157
AE > CE注:\为缺省值,引文未统计或计算该变量。 在涡旋极性对比方面,安达曼海反气旋涡AE数量多于气旋涡CE数量,这与南海[20]的结果较为一致,但与全球和孟加拉湾相反。并且,安达曼海AE比CE具有更强的振幅和更大的半径,而孟加拉湾[15-16]则CE比AE振幅大,而半径比AE旋小。考虑风场做功以及背景流涡度对涡旋极性影响,不同海域涡旋极性差异可能是不同海域的动力环境差异以及涡旋产生机制造成的[17]。
在传播方向方面,与其他海域一样,由于β效应的制约[23-24],安达曼海中尺度涡大部分向西移动。与西移的涡旋相比,东向移动涡旋的生命周期较短并且传播距离较近。这一结论与全球涡旋传播特征一致[44]。由于安达曼群岛和尼科巴群岛的存在,安达曼海中尺度涡大都在西部消亡,仅有少量涡旋能进入孟加拉湾,大部分涡旋传播距离不超过350 km。经向上,安达曼海反气旋涡运动有向赤道偏离的趋势,而气旋涡运动则有向极地偏离的趋势。这与全球及其他海域的结论一致。
5.2 关于风场对涡旋做功
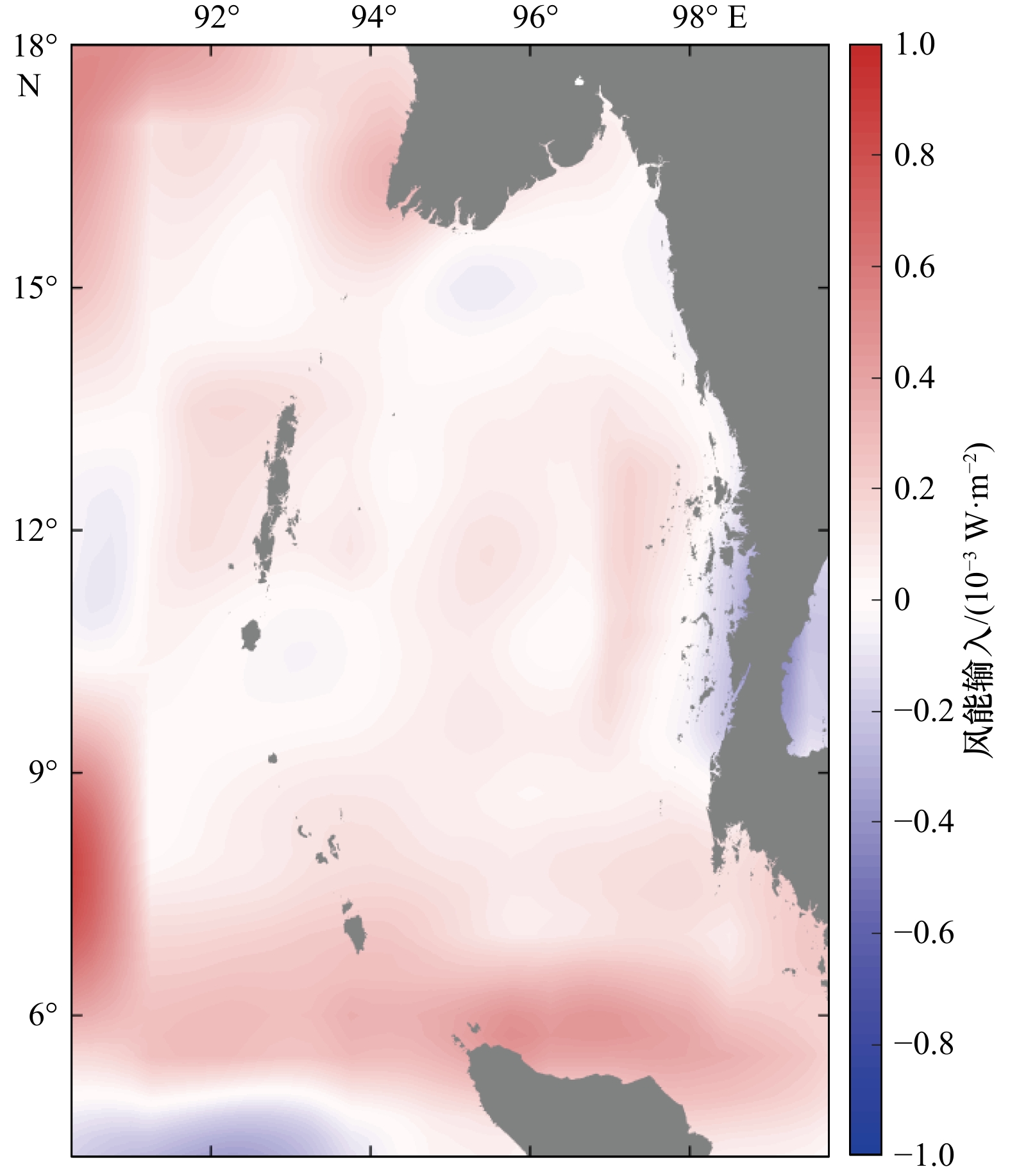
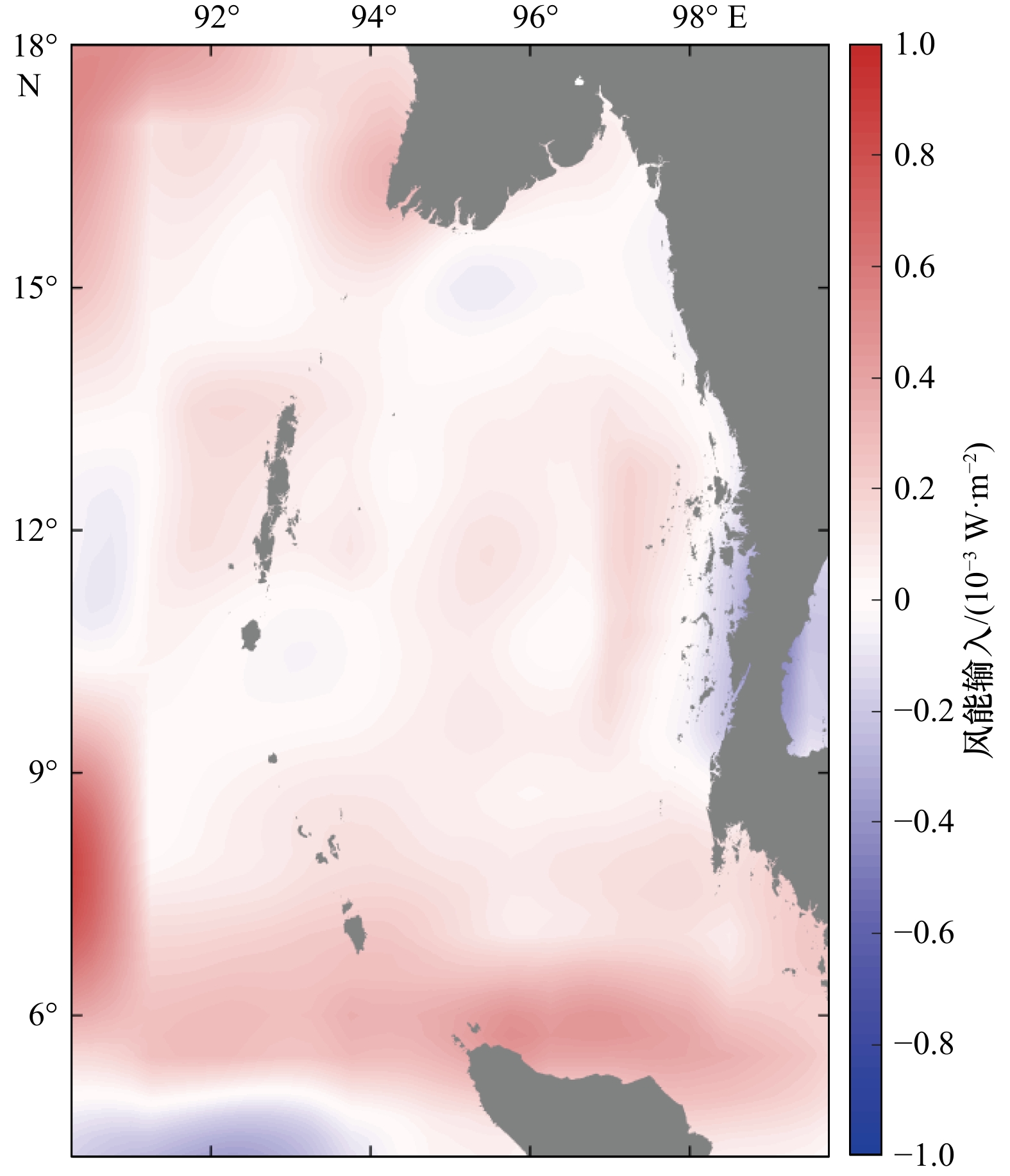
本文涡旋能量变化机制显示,风强迫是安达曼海涡旋主要能量来源。在风场做功时,我们采用了总风应力场与地转流速异常作用。最近,Rai等[45]利用卫星观测数据及基于空间滤波的多尺度解耦方法发现,在大于260 km的尺度上,全球平均的风对地转流做功为正,而在小于260 km的尺度上,风对地转流平均做负功,由此指出风是“涡旋杀手”(eddy killing)。需要指出的是,该结果是全球平均的结果,在南海和安达曼海等边缘海和靠近陆地的陆架海区,风场做功大多为正(参见Rai等[45]文中图2a)。图13为安达曼海在小于275 km尺度下的风能输入。可以看出,基于空间尺度分解的风能输入在安达曼海几乎全为正值,即风不断向中尺度涡输送能量,因此,本文结果与Rai等[45]结论一致。风能输入的量级在10−3 W/m2与4.4节中的WW量级一致,进一步说明了风强迫是安达曼海中尺度涡能量变化的主要机制。事实上,Teng等[46]最新研究发现,相对风应力不总是对涡旋做负功。他们基于一个仅考虑动量传递效应的简化理想模型发现,当涡旋结构独立于风场时,风应力在涡旋区上的积分做负功,但是当涡旋速度场适应风场时,风应力对涡旋做正功。这也反映了风场能量输入对中尺度涡速度场结构敏感。
6. 总结
本文利用 AVISO 提供的中尺度涡数据集,对1993−2019年间安达曼海中尺度涡的涡旋特征和时空变化进行了统计分析,主要结论如下:
(1)安达曼海在27 a间共产生中尺度涡328个,反气旋涡数量(171个)数量多于气旋涡(157个)。涡旋主要分布在安达曼海中北部海域、安达曼群岛附近海域和苏门答腊岛以北海域,而大都消亡于海盆西部安达曼群岛附近,部分涡旋进入东印度洋深水区。涡旋以较短寿命(<65 d)的涡旋为主,反气旋涡的平均半径、振幅和转速比气旋涡的稍大,而移动速度小于气旋涡。涡旋在移动过程中受β效应的约束纬向上主要是向西移动;经向上反气旋涡运动有向赤道偏离的趋势,而气旋涡运动则有向极地偏离的趋势。
(2)在生命周期中,涡旋半径、振幅和转速变化特征相似,均先增大后减小,涡旋移速则相反,先减小后增大。反气旋涡和气旋涡的生命周期演化特征类似。
(3)在季节变化方面,安达曼海中尺度反气旋和气旋涡数量、振幅和半径对比在冬夏两季呈“跷跷板”现象,即夏季气旋涡比反气旋涡更多更强更大,冬季则反气旋涡更多更强更大。春季和秋季为海区内涡旋位置变化的过渡期,无显著空间分布特征,但东侧存在一个反气旋聚集区;夏季涡旋极性分布从北向南呈“气旋−反气旋−气旋”的交替分布,冬季则与之相反。动力机制分析显示,背景流场涡度可能是影响安达曼海不同极性涡旋交替分布的机制。涡旋能量变化机制显示,风强迫是安达曼海涡旋主要能量来源,风场能量输入与涡旋动能EKE的季节变化吻合。
-
图 5 显著东移涡旋的生成位置(点)及对应的背景纬向流(a)和在西向背景流中显著东移涡旋的移动轨迹(b)
Fig. 5 The generation location of significant eastward propagating eddies (dots) and corresponding background zonal flow (a) and the significant eastward propagation trajectories of the cyclonic (orange lines) and anticyclonic (red lines) eddies in the westward background flow (b)
图 10 安达曼海夏(a)、冬(b)两季海面流场涡度(彩色)及涡旋生成位置(点)
实心红点为反气旋涡,实心蓝点为气旋涡。缩写C2 和AC3等指气旋或反气旋聚集发生区
Fig. 10 Background circulation vorticity (color) and eddy generating locations (dots) of Andaman Sea in summer (a) and winter (b)
Red and blue dots represent anticyclonic and cyclonic eddies, respectively. Abbreviations (i.e., C2, AC3) mark the cluster regions of cyclonic or anticyclonic eddies
表 1 涡旋纬向运动特征统计
Tab. 1 Statistical analysis of zonal motion characteristics
传播方向 涡旋极性 数量 占比 平均移动经度 空间分布 西向传播 AE 143 83.63% 1.72° 整个安达曼海 CE 116 73.89% 1.61° 东向传播 AE 28 16.37% 0.63° 安达曼海东部海域 CE 41 26.11% 0.71° 安达曼海西部海域 表 2 全球及安达曼海周边海域中尺度涡特征
Tab. 2 Mesoscale eddy characteristics of the world and the waters surrounding the Andaman Sea
海域 海域长宽(南北/东西)/km 生命周期/d 涡旋振幅/cm 涡旋半径/km 传播距离/km 不同极性数量比/AE∶CE 全球[35] >10000 84.9
AE > CE7.7
AE < CE82.4
AE > CE271.7
AE > CE173245∶179127
AE < CE孟加拉湾[15] 2750/1600 55
AE < CE9.2
AE < CE124
AE > CE336
AE < CE389∶565
AE < CE南海[20] 2000/1000 61.6 \ 132 582.5 434∶393
AE > CE班达海[13] 450/1000 40
AE < CE4.1
AE < CE116
AE=CE165.3
AE > CE71∶76
AE < CE苏禄海[40] 790/600 32 1.88 76.6 \ 225∶243
AE < CE安达曼海 1100/600 46.4
AE < CE4.7
AE > CE111.8
AE > CE231.3
AE > CE171∶157
AE > CE注:\为缺省值,引文未统计或计算该变量。 -
[1] 林宏阳, 胡建宇, 郑全安. 南海及西北太平洋卫星高度计资料分析: 海洋中尺度涡统计特征[J]. 台湾海峡, 2012, 31(1): 105−113.Lin Hongyang, Hu Jianyu, Zheng Quanan. Satellite altimeter data analysis of the South China Sea and the Northwest Pacific Ocean: statistical features of oceanic mesoscale eddies[J]. Journal of Oceanography in Taiwan Strait, 2012, 31(1): 105−113. [2] Richardson P L. Eddy kinetic energy in the North Atlantic from surface drifters[J]. Journal of Geophysical Research: Oceans, 1983, 88(C7): 4355−4367. [3] 修树孟, 郑全安, 孙湘平. 中尺度涡诱导的陆架上升流[J]. 水动力学研究与进展(A辑), 2002, 17(1): 61−68.Xiu Shumeng, Zheng Quanan, Sun Xiangping. Shelf upwelling induced by mesoscale eddy[J]. Journal of Hydrodynamics (Ser. A), 2002, 17(1): 61−68. [4] 李敏, 谢玲玲, 杨庆轩, 等. 湾流区涡旋对海洋垂向混合的影响[J]. 中国科学: 地球科学, 2014, 44(4): 744−752.Li Min, Xie Lingling, Yang Qingxuan, et al. Impact of eddies on ocean diapycnal mixing in gulf stream region[J]. Science China Earth Sciences, 2014, 44(4): 744−752. [5] 刘金. 南海北部跨陆架输运的变化及中尺度涡对叶绿素的影响[D]. 杭州: 浙江大学, 2019.Liu Jin. Variations of cross-shelf volume transports and mesoscale eddy effects on Chlorophyll in the northern South China Sea[D]. Hangzhou: Zhejiang University, 2019. [6] Farneti R, Delworth T L, Rosati A J, et al. The role of mesoscale eddies in the rectification of the Southern Ocean response to climate change[J]. Journal of Physical Oceanography, 2010, 40(7): 1539−1557. doi: 10.1175/2010JPO4353.1 [7] Jian Yongjun, Zhang J, Liu Quansheng, et al. Effect of mesoscale eddies on underwater sound propagation[J]. Applied Acoustics, 2009, 70(3): 432−440. doi: 10.1016/j.apacoust.2008.05.007 [8] 汤博. 中尺度涡旋的统计特征及其温盐场的反演方法研究[D]. 青岛: 中国科学院大学(中国科学院海洋研究所), 2019.Tang Bo. A study on the statistical characteristic of mesoscale eddies and the inversion method of their temperature and salinity fields[D]. Qingdao: The Institute of Oceanology, Chinese Academy of Sciences, 2019. [9] Babu M T, Kumar P S, Rao D P. A subsurface cyclonic eddy in the Bay of Bengal[J]. Journal of Marine Research, 1991, 49(3): 403−410. doi: 10.1357/002224091784995846 [10] Sanilkumar K V, Kuruvilla T V, Jogendranath D, et al. Observations of the Western Boundary Current of the Bay of Bengal from a hydrographic survey during March 1993[J]. Deep-Sea Research Part I: Oceanographic Research Papers, 1997, 44(1): 135−145. doi: 10.1016/S0967-0637(96)00036-2 [11] 郑全安, 张朝贤. 全球尺度海洋学研究对卫星遥感数据的需求[J]. 黄渤海海洋, 1989, 7(2): 53−58.Zheng Quanan, Zhang Chaoxian. Requirements of global scale oceanographic study for satellite remote sensing data[J]. Journal of Oceanography of Huanghai & Bohai Seas, 1989, 7(2): 53−58. [12] 郑全安, 谢玲玲, 郑志文, 等. 南海中尺度涡研究进展[J]. 海洋科学进展, 2017, 35(2): 131−158. doi: 10.3969/j.issn.1671-6647.2017.02.001Zheng Quanan, Xie Lingling, Zheng Zhiwen, et al. Progress in research of mesoscale eddies in the South China Sea[J]. Advances in Marine Science, 2017, 35(2): 131−158. doi: 10.3969/j.issn.1671-6647.2017.02.001 [13] Chen Baiyang, Xie Lingling, Zheng Quanan, et al. Seasonal variability of mesoscale eddies in the Banda Sea inferred from altimeter data[J]. Acta Oceanologica Sinica, 2020, 39(12): 11−20. doi: 10.1007/s13131-020-1665-2 [14] Chen Gengxin, Wang Dongxiao, Hou Yijun, et al. The features and interannual variability mechanism of mesoscale eddies in the Bay of Bengal[J]. Continental Shelf Research, 2012: 178−185. [15] Cui Wei, Yang Jungang, Ma Yi. A statistical analysis of mesoscale eddies in the Bay of Bengal from 22-year altimetry data[J]. Acta Oceanologica Sinica, 2016, 35(11): 16−27. doi: 10.1007/s13131-016-0945-3 [16] 常景龙, 邱云, 林新宇, 等. 孟加拉湾中尺度涡的总体特征与季节变化[J]. 应用海洋学学报, 2019, 38(2): 149−158. doi: 10.3969/J.ISSN.2095-4972.2019.02.001Chang Jinglong, Qiu Yun, Lin Xinyu, et al. General features and seasonal variation of mesoscale eddies in the Bay of Bengal[J]. Journal of Applied Oceanography, 2019, 38(2): 149−158. doi: 10.3969/J.ISSN.2095-4972.2019.02.001 [17] 黄挺, 周锋, 田娣, 等. 孟加拉湾及其毗邻海域中尺度涡旋活动的冬、夏季差异[J]. 海洋学研究, 2020, 38(3): 21−30. doi: 10.3969/j.issn.1001-909X.2020.03.003Huang Ting, Zhou Feng, Tian Di, et al. Seasonal variations of mesoscale eddy in the Bay of Bengal and its adjacent regions[J]. Journal of Marine Sciences, 2020, 38(3): 21−30. doi: 10.3969/j.issn.1001-909X.2020.03.003 [18] 周礼英. 基于遥感影像的安达曼海及其邻近海域内波分析[D]. 杭州: 浙江大学, 2018.Zhou Liying. Analysis of internal waves in the Andaman Sea and its adjacent waters based on remote sensing images[D]. Hangzhou: Zhejiang University, 2018. [19] Schlax M G, Chelton D B. The “growing method” of eddy identification and tracking in two and three dimensions[R]. College of Earth, Ocean and Atmospheric Sciences, Oregon State University, Corvallis, Oregon, 2016. [20] Chen Gengxin, Hou Yijun, Chu Xiaoqing. Mesoscale eddies in the South China Sea: mean properties, spatiotemporal variability, and impact on thermohaline structure[J]. Journal of Geophysical Research: Ocenas, 2011, 116(C6): C06018. [21] Cheng Y H, Ho C R, Zheng Quanan, et al. Statistical characteristics of mesoscale eddies in the North Pacific derived from satellite altimetry[J]. Remote Sensing, 2014, 6(6): 5164−5183. doi: 10.3390/rs6065164 [22] Huang Runqi, Xie Lingling, Zheng Quanan, et al. Statistical analysis of mesoscale eddy propagation velocity in the South China Sea deep basin[J]. Acta Oceanologica Sinica, 2020, 39(11): 91−102. doi: 10.1007/s13131-020-1678-x [23] Nof D. On the β-induced movement of isolated baroclinic eddies[J]. Journal of Physical Oceanography, 1981, 11: 1662−1672. doi: 10.1175/1520-0485(1981)011<1662:OTIMOI>2.0.CO;2 [24] Cushman-Roisin B, Tang Benyang, Chassignet E P. Westward motion of mesoscale eddies[J]. Journal of Physical Oceanography, 1990, 20(5): 758−768. doi: 10.1175/1520-0485(1990)020<0758:WMOME>2.0.CO;2 [25] Peng Lin, Chen Ge, Guan Lei, et al. Contrasting westward and eastward propagating mesoscale eddies in the global ocean[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 60: 4504710. [26] Chelton D B, Schlax M G, Samelson R M, et al. Global observations of large oceanic eddies[J]. Geophysical Research Letters, 2007, 34(15): L15606. [27] Shi Y, Yang D, Feng X, et al. One possible mechanism for eddy distribution in zonal current with meridional shear[J]. Scientific Reports, 2018, 8(1): 1−9. [28] Lin X, Qiu Y, Sun D. Thermohaline structures and heat/freshwater transports of mesoscale eddies in the Bay of Bengal observed by Argo and satellite data[J]. Remote Sensing, 2019, 11(24): 2989. doi: 10.3390/rs11242989 [29] Zhang Z, Zhao W, Qiu B, et al. Anticyclonic eddy sheddings from Kuroshio loop and the accompanying cyclonic eddy in the northeastern South China Sea[J]. Journal of Physical Oceanography, 2017, 47(6): 1243−1259. doi: 10.1175/JPO-D-16-0185.1 [30] Chen G, Li Y, Xie Q, et al. Origins of eddy kinetic energy in the Bay of Bengal[J]. Journal of Geophysical Research: Oceans, 2018, 123(3): 2097−2115. doi: 10.1002/2017JC013455 [31] Cheng X, McCreary J P, Qiu B, et al. Intraseasonal-to-semiannual variability of sea-surface height in the eastern, equatorial Indian Ocean and southern Bay of Bengal[J]. Journal of Geophysical Research: Oceans, 2017, 122(5): 4051−4067. doi: 10.1002/2016JC012662 [32] Rao R R, Kumar M S G, Ravichandran M, et al. Interannual variability of Kelvin wave propagation in the wave guides of the equatorial Indian Ocean, the coastal Bay of Bengal and the southeastern Arabian Sea during 1993–2006[J]. Deep-Sea Research Part I: Oceanographic Research Papers, 2010, 57(1): 1−13. doi: 10.1016/j.dsr.2009.10.008 [33] Ubelmann C, Fu L. Cyclonic eddies formed at the Pacific tropical instability wave fronts[J]. Journal of Geophysical Research: Oceans, 2011, 116(C12). [34] Xie L, Zheng Q, Zhang S, et al. The Rossby normal modes in the South China Sea deep basin evidenced by satellite altimetry[J]. International Journal of Remote Sensing, 2018, 39(2): 399−417. doi: 10.1080/01431161.2017.1384591 [35] Tian F, Wu D, Yuan L, et al. Impacts of the efficiencies of identification and tracking algorithms on the statistical properties of global mesoscale eddies using merged altimeter data[J]. International Journal of Remote Sensing, 2020, 41(8): 2835−2860. doi: 10.1080/01431161.2019.1694724 [36] 崔伟, 王伟, 马毅, 等. 基于1993—2014年高度计数据的西北太平洋中尺度涡识别和特征分析[J]. 海洋学报, 2017, 39(2): 16−28.Cui Wei, Wang Wei, Ma Yi, et al. Identification and analysis of mesoscale eddies in the northwestern Pacific Ocean from 1993–2014 based on altimetry data[J]. Haiyang Xuebao, 2017, 39(2): 16−28. [37] 胡冬, 陈希, 毛科峰, 等. 南印度洋中尺度涡统计特征及三维合成结构研究[J]. 海洋学报, 2017, 39(9): 1−14.Hu D, Chen X, Mao K, et al. Statistical characteristics and composed three dimensional structures of mesoscale eddies in the South Indian Ocean[J]. Haiyang Xuebao, 2017, 39(9): 1−14. [38] Scharffenberg M G, Stammer D. Annual variations of geostrophic currents and eddy kinetic energy inferred from TOPEX/Poseidon and Jason-1 tandem mission data[C]. Orlando: European Organisation for the Exploitation of Meteorological Satellites. 2008: 3−7. [39] Qiu B, Chen S. Interannual variability of the North Pacific Subtropical Countercurrent and its associated mesoscale eddy field[J]. Journal of Physical Oceanography, 2010, 40(1): 213−225. doi: 10.1175/2009JPO4285.1 [40] He Y, Feng M, Xie J, et al. Spatiotemporal variations of mesoscale eddies in the Sulu Sea[J]. Journal of Geophysical Research: Oceans, 2017, 122(10): 7867−7879. doi: 10.1002/2017JC013153 [41] Hao Z, Xu Z, Feng M, et al. Spatiotemporal variability of mesoscale eddies in the Indonesian Seas[J]. Remote Sensing, 2021, 13(5): 1017. doi: 10.3390/rs13051017 [42] Zhan P, Subramanian A C, Yao F, et al. Eddies in the Red Sea: A statistical and dynamical study[J]. Journal of Geophysical Research: Oceans, 2014, 119(6): 3909−3925. doi: 10.1002/2013JC009563 [43] Chen G, Han G. Contrasting short-lived with long-lived mesoscale eddies in the global ocean[J]. Journal of Geophysical Research: Oceans, 2019, 124(5): 3149−3167. doi: 10.1029/2019JC014983 [44] Chelton D, Schlax M, Samelson R. Global observations of nonlinear mesoscale eddies[J]. Progress in Oceanography, 2011, 91(2): 167−216. doi: 10.1016/j.pocean.2011.01.002 [45] Rai S, Hecht M, Maltrud M, et al. Scale of oceanic eddy killing by wind from global satellite observations[J]. Science Advances, 2021, 7(28): eabf4920. doi: 10.1126/sciadv.abf4920 [46] Teng F, Dong C, Ji J, et al. Does the wind stress always damp an oceanic eddy?[J]. Geoscience Letters, 2021, 8(1): 1−6. doi: 10.1186/s40562-020-00170-8 -






 下载:
下载:
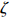
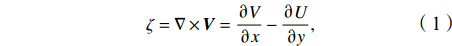
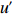
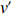
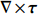
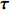
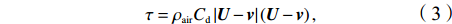
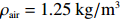
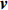







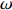
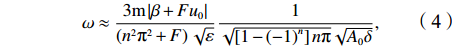
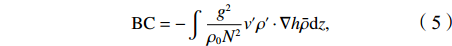
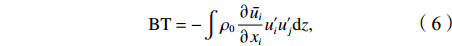
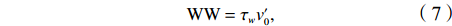




 下载:
下载: