Generation and evolution on symmetric ocean inner waves in unstable background flow
-
摘要: 本文采用无海底地形但考虑海洋跃层和剪切背景流的二维非静力准不可压缩方程组的数值模式,开展失稳垂向剪切背景流下线性和非线性对称型海洋内波生成演变的数值实验,并对结果进行分析、比较和讨论。研究结果表明,线性内波强度随积分时间始终呈指数增长,并有内波的对称不稳定;而非线性内波强度则在发展期呈准线性增长,最终进入稳定期。线性增长比非线性增长要快得多,非线性效应具有维稳作用。对该线性和非线性对称型内波,在跃层附近位密度扰动均有大值中心,即其为跃层所俘获,这与实际观测相一致;流函数与位密度扰动两者均有很好配合,位密度扰动的正、负中心分别相应于流函数的上升、下沉运动,表明有从海底向上的斜对流发生,且以跃层为顶盖。对线性内波来说,随积分时间增加,其波形大体不变,其正、负振幅也大体相同,并有符号相反原地增长的两个倾斜环流圈,而在它们之间则有较强倾斜上升流。非线性内波波形随积分时间改变,倾斜环流圈数目也在增加,最终形成负环流强于正环流的结果,并导致流函数、位密度扰动水平梯度剧增,其可视为间断。Abstract: Using the two-dimensional non-static numerical model, which neglect the submarine topography but consider the pycnocline and background shear flow, the numerical experiment was made on the generation and evolution of linear and nonlinear symmetric ocean internal waves in the unstable downward shear background flow. After analyzing and comparing the results, the main conclusions are as follows: the linear internal wave strength is exponentially growing with integral time, and there’s symmetric instability of the wave, while nonlinear internal wave strength is growing quasi-linearly in the development stage, and finally enters the stabilization stage. The linear growing is much faster than the nonlinear growing and the latter has a stabilizing effect. For linear and nonlinear symmetric internal waves, there are maximum value of potential density perturbation, which is captured by the pycnocline. This is consistent with actual observations. The stream function and potential density perturbation are well coordinated, which is reflected in the positive and negative centers of the potential density perturbation corresponding to the rising and sinking movements of the stream function, respectively. This shows that there is a slantwise convection occurred from the bottom of the sea and the pycnocline is the top cover. For linear internal waves, with the increase of integral time, its waveform is basically the same and the positive and negative amplitude is also about the same. There are two slantwise circulations that grow in opposite signs and between them is a strong slantwise upwelling. The waveform of nonlinear internal wave changes with the integration time and the number of slantwise circulations is also increasing, resulting in the stronger negative circulations and a sharp increase in the horizontal gradient of stream function and potential density perturbation. The sharp increase can be regarded as an interruption.
-
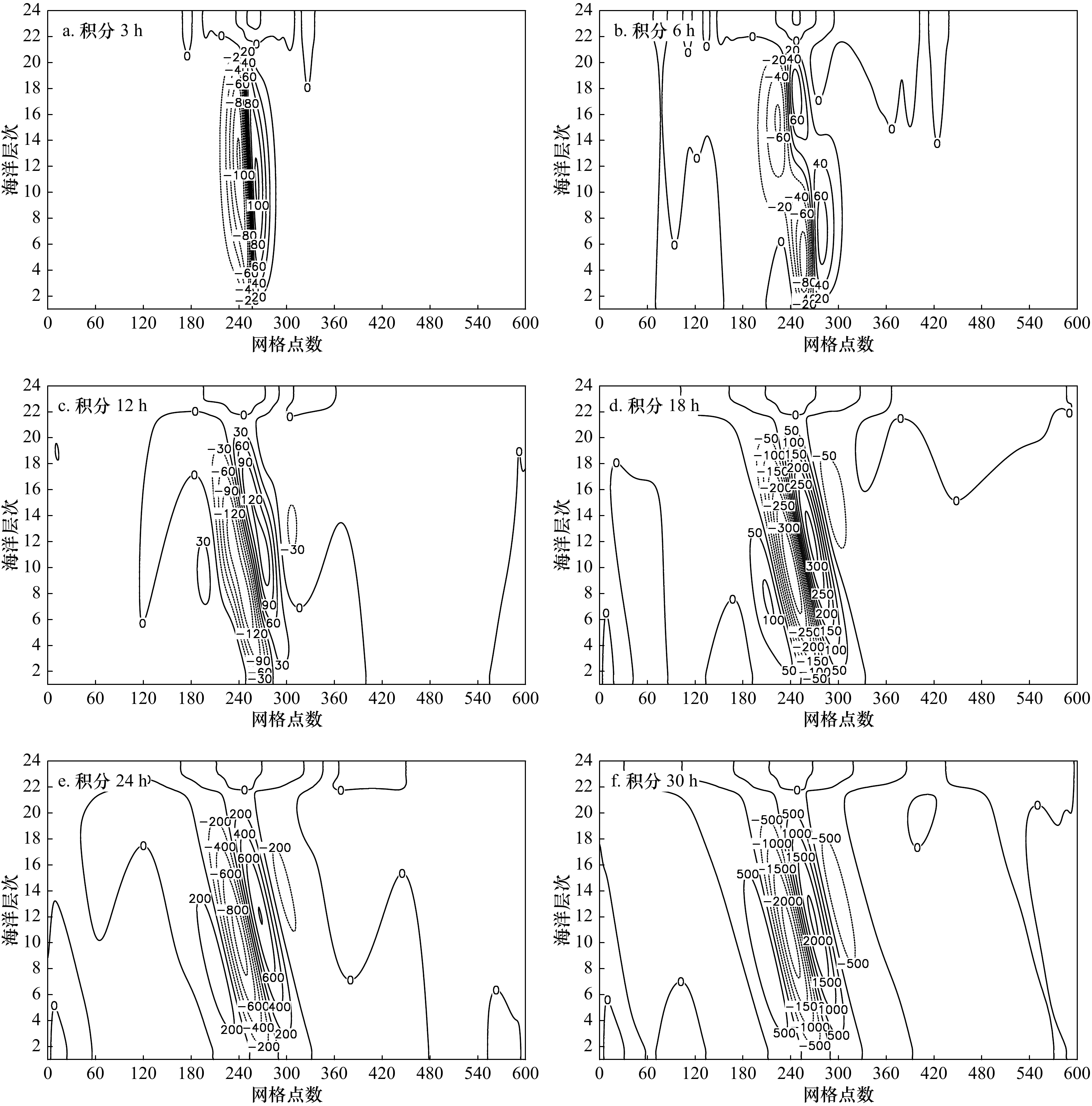
图 2 线性模型中流函数的空间分布(等值线表示流函数,单位:m2/s)
水平格距为80 m,海洋层次第1层为海底,第24层为海面,层距为80 m
Fig. 2 The distribution of stream functions in linear models (isolines represent stream functions, unit: m2/s)
The horizontal grid distance is 80 m, the first layer is the sea floor, the 24th layer is the sea surface, the layer distance is 80 m
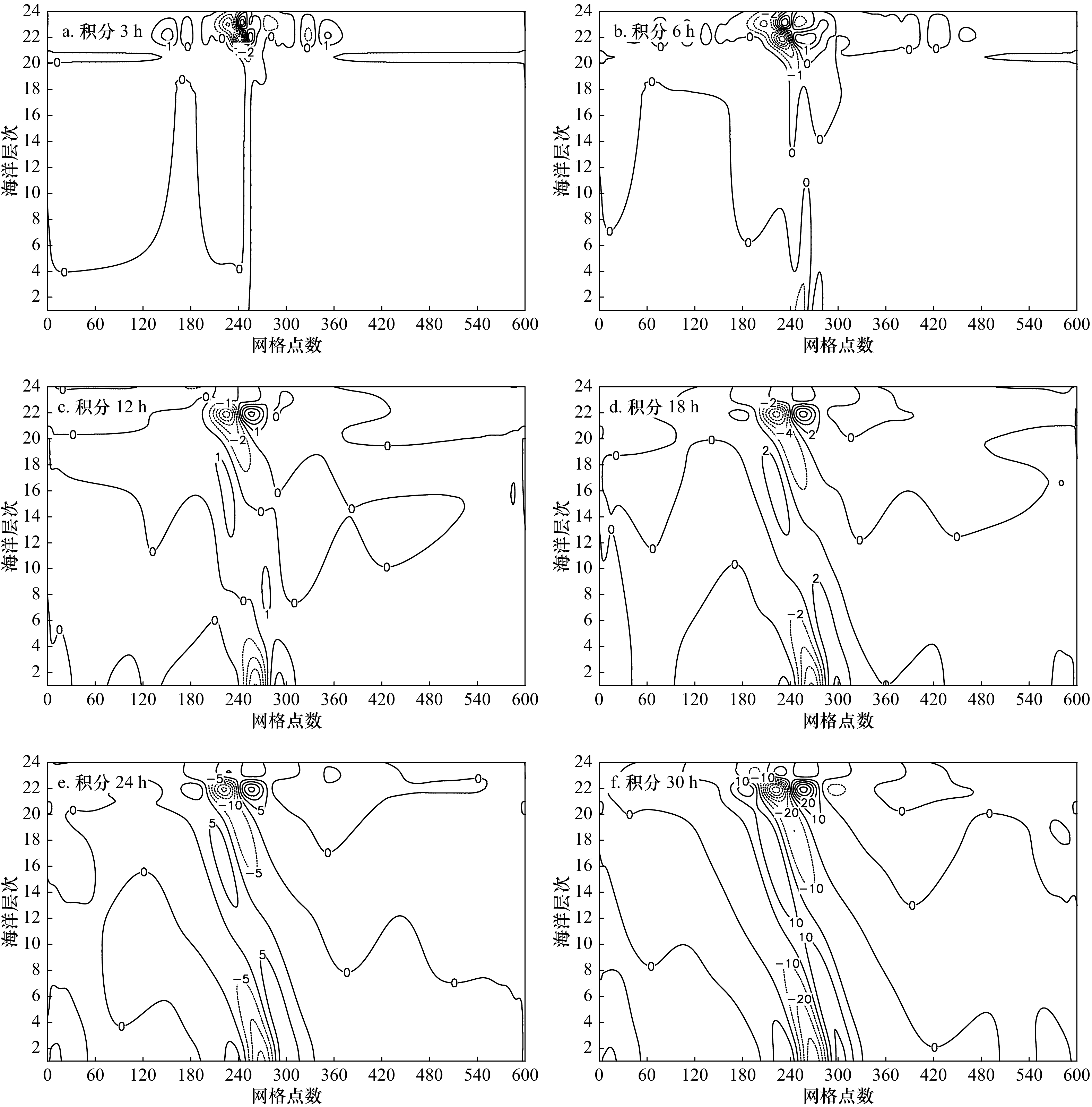
图 3 线性模型中位密度扰动场的空间分布(等值线表示位密度,单位:10−4 m/s2)
水平格距为80 m,海洋层次第1层为海底,第24层为海面,层距为80 m
Fig. 3 The distribution of potential density perturbation in linear models (isolines represent potential density, unit: 10−4 m/s2)
The horizontal grid distance is 80 m, the first layer is the sea floor, the 24th layer is the sea surface, the layer distance is 80 m
图 4 非线性模型中流函数的空间分布(等值线表示流函数,单位:m2/s)
水平格距为80 m,海洋层次第1层为海底,第24层为海面,层距为80 m
Fig. 4 The distribution of streamfunctions in nonlinear models (isolines represent stream function, unit: m2/s)
The horizontal grid distance is 80 m, the first layer is the sea floor, the 24th layer is the sea surface, the layer distance is 80 m
图 5 非线性模型中位密度场的空间分布(等值线表示位密度,单位10−4 m/s2)
水平格距为80 m,海洋层次第1层为海底,第24层为海面,层距为80 m
Fig. 5 The distribution of potential density perturbation fields in nonlinear models (isolines represent potential density, unit: 10−4 m/s2)
The horizontal grid distance is 80 m, the first layer is the sea floor, the 24th layer is the sea surface, the layer distance is 80 m
-
[1] 方欣华, 杜涛. 海洋内波基础和中国海内波[M]. 青岛: 中国海洋大学出版社, 2005.Fang Xinhua, Du Tao. Fundamentals of Oceanic Internal Waves and Internal Waves in the China Seas[M]. Qingdao: China Ocean University Press, 2005. [2] Guo Daquan, Zhan Peng, Kartadikaria A R, et al. On the generation and evolution of internal solitary waves in the southern Red Sea[C]//EGU General Assembly 2015. Vienna, Austria: EGU, 2015. [3] Bulatov V V, Vladimirov Y V. Internal gravity waves in horizontally inhomogeneous ocean[M]//Velarde M, Tarakanov R, Marchenko A. The Ocean in Motion. Cham: Springer, 2018: 109−126. [4] Mathur M. Simultaneous generation and scattering of internal tides by ocean floor topography[C]//68th Annual Meeting of the APS Division of Fluid Dynamics. Boston, Massachusetts: APS, 2015. [5] 王金虎, 陈旭, 徐洋. 粗糙地形对内波生成影响的实验研究[J]. 海洋与湖沼, 2016, 47(4): 706−713. doi: 10.11693/hyhz20160100006Wang Jinhu, Chen Xun, Xu Yang. Laboratory study on internal wave generation in rough topography[J]. Oceanologia et Limnologia Sinica, 2016, 47(4): 706−713. doi: 10.11693/hyhz20160100006 [6] Moum J N, Farmer D M, Smyth W D, et al. Structure and generation of turbulence at interfaces strained by internal solitary waves propagating shoreward over the continental shelf[J]. Journal of Physical Oceanography, 2003, 33(10): 2093−2112. doi: 10.1175/1520-0485(2003)033<2093:SAGOTA>2.0.CO;2 [7] Kalashnik M V. Generation of internal gravity waves by vortex disturbances in a shear flow[J]. Izvestiya, Atmospheric and Oceanic Physics, 2014, 50(6): 638−647. doi: 10.1134/S0001433814060115 [8] Mack A P, Hebert D. Mixing structure of high-frequency internal waves in the upper eastern equatorial Pacific[J]. Journal of Physical Oceanography, 1999, 29(12): 3090−3100. doi: 10.1175/1520-0485(1999)029<3090:MSOHFI>2.0.CO;2 [9] Lozovatsky I. Internal waves and shear instability in the southern bay of Bengal[R]. American Geophysical Union, Ocean Sciences Meeting 2016. 2016. [10] Zhang Shuang, Alford M H. Instabilities in nonlinear internal waves on the Washington continental shelf[J]. Journal of Geophysical Research: Oceans, 2015, 120(7): 5272−5283. [11] Yuan Yeli, Wan Zhenwen, Zhang Qinghua. A motion instability formation mechanism of the multi-core structure of the East China Sea Kuroshio[J]. Science in China Series D: Earth Sciences, 2003, 46(2): 182−192. doi: 10.1360/03yd9017 [12] Yuan Yeli, Zheng Quanan, Dai Dejun, et al. The mechanism of internal waves in the Luzon Strait[J]. Journal of Geophysical Research: Oceans, 2006, 111(C11): C11S17. [13] 张铭, 张立凤, 安洁. 大气波谱分析及其不稳定性[M]. 北京: 气象出版社, 2008.Zhang Ming, Zhang Lifeng, An Jie. The Spectrum Analysis and Instability of Atmospheric Wave[M]. Beijing: Meteorological Press, 2008. [14] 穆穆. 大气运动的非线性稳定与不稳定问题研究[J]. 中国科学院院刊, 2001, 16(6): 432−435. doi: 10.3969/j.issn.1000-3045.2001.06.008Mu Mu. Nonlinear stability and instability of atmospheric motions[J]. Bulletin of the Chinese Academy of Sciences, 2001, 16(6): 432−435. doi: 10.3969/j.issn.1000-3045.2001.06.008 [15] Ai Congfang, Ding Weiye. A 3D unstructured non-hydrostatic ocean model for internal waves[J]. Ocean Dynamics, 2016, 66(10): 1253−1270. doi: 10.1007/s10236-016-0980-9 [16] 张翔, 邓冰, 张铭, 等. 背景流与地形对海洋内波影响初探[J]. 海洋预报, 2012, 29(3): 26−35. doi: 10.3969/j.issn.1003-0239.2012.03.005Zhang Xiang, Deng Bing, Zhang Ming, et al. Preliminary study of background current and topography offects on ocean internal wave[J]. Marine Forecasts, 2012, 29(3): 26−35. doi: 10.3969/j.issn.1003-0239.2012.03.005 [17] 邓冰, 张宇飞, 张铭. 海洋内波发展演变数值试验[J]. 海洋科学进展, 2017, 35(1): 62−72. doi: 10.3969/j.issn.1671-6647.2017.01.007Deng Bing, Zhang Yufei, Zhang Ming. Numerical experiments of oceanic internal wave evolution[J]. Advances in Marine Science, 2017, 35(1): 62−72. doi: 10.3969/j.issn.1671-6647.2017.01.007 [18] 邓冰, 张铭. 海洋内部波动的波谱和谱函数I·数学模型和计算方法[J]. 水动力学研究与进展A辑, 2006, 21(2): 259−266. doi: 10.3969/j.issn.1000-4874.2006.02.016Deng Bing, Zhang Ming. Spectrum and spectral function analysis of wave in ocean Part I·mathematic model and numerical method[J]. Journal of Hydrodynamics, 2006, 21(2): 259−266. doi: 10.3969/j.issn.1000-4874.2006.02.016 [19] Alford M H, Peacock T, MacKinnon J A, et al. The formation and fate of internal waves in the South China Sea[J]. Nature, 2015, 521(7550): 65−69. doi: 10.1038/nature14399 [20] Kurkina O E, Kurkin A A, Pelinovsky E N, et al. Structure of currents in the soliton of an internal wave[J]. Oceanology, 2016, 56(6): 767−773. doi: 10.1134/S0001437016060072 [21] 邓冰, 张宇飞, 朱娟, 等. 海洋剪切流下失稳内波流场及传播的理论分析[J]. 海洋预报, 2016, 33(3): 1−8. doi: 10.11737/j.issn.1003-0239.2016.03.001Deng Bing, Zhang Yufei, Zhu Juan, et al. Theoretical analysis on the stream structure and propagation of unstable ocean internal wave at background shear flow[J]. Marine Forecasts, 2016, 33(3): 1−8. doi: 10.11737/j.issn.1003-0239.2016.03.001 [22] 邓冰, 张翔, 张铭. 背景流中海洋内波垂向结构的计算和分析[J]. 海洋科学进展, 2014, 32(2): 121−129. doi: 10.3969/j.issn.1671-6647.2014.02.001Deng Bing, Zhang Xiang, Zhang Ming. Calculation and analysis of vertical structure of internal wave in background current[J]. Advances in Marine Science, 2014, 32(2): 121−129. doi: 10.3969/j.issn.1671-6647.2014.02.001 [23] Zhang Yufei, Deng Bing, Zhang Ming. Analysis of the relation between ocean internal wave parameters and ocean surface fluctuation[J]. Frontiers of Earth Science, 2019, 13(2): 336−350. doi: 10.1007/s11707-018-0735-7 [24] 张立凤, 张铭. 非均匀层结下的对称不稳定[J]. 大气科学, 1997, 21(5): 627−632. doi: 10.3878/j.issn.1006-9895.1997.05.14Zhang Lifeng, Zhang Ming. Symmetric instability in nonhomogeneous stratification[J]. Chinese Journal of Atmospheric Sciences, 1997, 21(5): 627−632. doi: 10.3878/j.issn.1006-9895.1997.05.14 [25] Huang Sixun, Zhang Ming. Study on atmospheric travelling wave solutions and review of its present developments[J]. Advances in Atmospheric Science, 1993, 10(4): 435−446. doi: 10.1007/BF02656968 -




 下载:
下载: